Section A: 1 mark questions

Q1: Find the cofactor of $a_{12}$ in the following: $\begin{vmatrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{vmatrix}$

(a) -46

(b) 46

(d) 1

Solution:
To find the cofactor of an element in a determinant, we use the formula:
$A_{ij} = (-1)^{i+j} M_{ij}$
Where:
$A_{ij}$ is the cofactor of the element in the $i^{th}$ row and $j^{th}$ column.
$M_{ij}$ is the minor of the element, obtained by deleting the $i^{th}$ row and $j^{th}$ column.

Step 1: Identify the element and its position.
We need to find the cofactor of $a_{12}$ .
Here, $i = 1$ (First Row) and $j = 2$ (Second Column).

Step 2: Determine the sign.
Using the formula $(-1)^{i+j}$ :
$(-1)^{1+2} = (-1)^3 = -1$

So, the cofactor will have a negative sign attached to the minor.

Step 3: Calculate the Minor ( $M_{12}$ ).
Eliminate the first row and the second column from the given determinant:
$\begin{vmatrix} \mathbf{2} & \mathbf{-3} & \mathbf{5} \\ 6 & \mathbf{0} & 4 \\ 1 & \mathbf{5} & -7 \end{vmatrix} \longrightarrow \begin{vmatrix} 6 & 4 \\ 1 & -7 \end{vmatrix}$

Now, calculate the value of this 2×2 determinant:
$M_{12} = (6 \times -7) - (4 \times 1)$
$M_{12} = (-42) - (4)$
$M_{12} = -46$

Step 4: Calculate the Cofactor ( $A_{12}$ ).
Combine the sign from Step 2 and the minor from Step 3:
$A_{12} = (-1) \times (-46)$
$A_{12} = 46$

The cofactor of $a_{12}$ is 46.

Correct Option: (b)

Q2: If $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 3 & 1 \\ 2 & 5 \end{bmatrix} = \begin{bmatrix} 7 & 11 \\ k & 23 \end{bmatrix}$ , then write the value of k.

(a) 17

(b) -17

(d) -13

Solution: To find the value of $k$ , we need to perform matrix multiplication on the Left Hand Side (LHS) and equate the corresponding element to the Right Hand Side (RHS).

Step 1: Identify the position of k.
In the RHS matrix $\begin{bmatrix} 7 & 11 \\ k & 23 \end{bmatrix}$ , the variable $k$ is in the 2nd Row, 1st Column ( $a_{21}$ ).

Step 2: Calculate the element $a_{21}$ from the LHS.
We multiply the 2nd Row of the first matrix by the 1st Column of the second matrix.
Row 2 of Matrix 1: $[3, 4]$ Column 1 of Matrix 2: $\begin{bmatrix} 3 \\ 2 \end{bmatrix}$

Calculation:
$a_{21} = (3 \times 3) + (4 \times 2)$
$a_{21} = 9 + 8$
$a_{21} = 17$

Step 3: Equate to find k.
Since the matrices are equal, their corresponding elements must be equal.
$k = 17$

Correct Option: (a)

Q3: If $y = \sqrt{a^{2}-x^{2}}$ , then $y\frac{dy}{dx}$ is:

(a) 0

(b) x

(d) 1

Solution: We need to find the value of the expression $y\frac{dy}{dx}$ given the function for $y$ .
Step 1: Differentiate $y$ with respect to $x$ .
Given:
$y = \sqrt{a^{2}-x^{2}}$
$y = (a^{2}-x^{2})^{1/2}$

Using the Chain Rule:
$\frac{dy}{dx} = \frac{1}{2} (a^{2}-x^{2})^{1/2} \times \frac{d}{dx} (a^2 - x^2)$

$\frac{dy}{dx} = \frac{1}{2\sqrt{a^2 - x^2}} \times (0 - 2x)$

$\frac{dy}{dx} = \frac{-2x}{2\sqrt{a^2 - x^2}}$

$\frac{dy}{dx} = \frac{-x}{\sqrt{a^2 - x^2}}$

Step 2: Substitute $y$ back into the derivative.
Since $y = \sqrt{a^2 - x^2}$ , we can substitute the denominator:

$\frac{dy}{dx} = \frac{-x}{y}$

Step 3: Calculate $y\frac{dy}{dx}$ .
Multiply both sides by $y$ :
$y\frac{dy}{dx} = -x$

Correct Option: (c)

Q4: If $f(x)=x^{2}sin\frac{1}{x}$ where $x\ne0$ , then the value of the function f at $x=0$ so that the function is continuous at $x=0$ is:

(a) 0

(b) -1

(d) None of these

Solution:
For a function to be continuous at a point $x = c$ , the limit of the function as $x \to c$ must equal the value of the function at that point.

Condition for continuity at $x = 0$ :
$\lim_{x \to 0} f(x) = f(0)$

Step 1: Evaluate the limit.
We need to find $\lim_{x \to 0} \left( x^2 \sin\frac{1}{x} \right)$ .

We know that the range of the sine function is always between -1 and 1:
$-1 \le \sin\frac{1}{x} \le 1$

Multiply the inequality by $x^2$ (which is always non-negative):
$-x^2 \le x^2 \sin\frac{1}{x} \le x^2$

Step 2: Apply the Squeeze Theorem (Sandwich Theorem).
Take the limit as $x \to 0$ for the outer terms:

$\lim_{x \to 0} (-x^2) = 0$

$\lim_{x \to 0} (x^2) = 0$

Since the function $x^2 \sin\frac{1}{x}$ is “squeezed” between two functions that both approach 0, the limit is:
$\lim_{x \to 0} \left( x^2 \sin\frac{1}{x} \right) = 0$

Step 3: Determine $f(0)$ .
For continuity, $f(0)$ must equal the limit.

$f(0) = 0$

Correct Option: (a)

Q5: The value of $\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{dx}{1+\sqrt{\tan x}}$ is:

(a) $\pi/6$

(b) 0

(d) None of these

Solution:
Step 1: Use the property of definite integrals.
Property: $\int_{a}^{b} f(x) dx = \int_{a}^{b} f(a+b-x) dx$

Here, $a = \frac{\pi}{6}$ and $b = \frac{\pi}{3}$ .

Sum of limits: $a + b = \frac{\pi}{6} + \frac{\pi}{3} = \frac{\pi}{2}$ (90 degrees).

Step 2: Apply the property to the integral.
Let $I = \int_{\pi/6}^{\pi/3}\frac{dx}{1+\sqrt{\tan x}}$ … (i)

Using the property $x \to (\frac{\pi}{2} - x)$ : Since $\tan(\frac{\pi}{2}-x) = \cot x = \frac{1}{\tan x}$ :
$I = \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{dx}{1+\sqrt{\cot x}}$

$I = \int_{\pi/6}^{\pi/3}\frac{dx}{1+\frac{1}{\sqrt{\tan x}}}$

$I = \int_{\pi/6}^{\pi/3}\frac{\sqrt{\tan x}}{1+\sqrt{\tan x}} dx$ … (ii)

Step 3: Add equations (i) and (ii).
$2I = \int_{\pi/6}^{\pi/3} \left( \frac{dx}{1+\sqrt{\tan x}} + \frac{\sqrt{\tan x}}{1+\sqrt{\tan x}} \right) dx$

$2I = \int_{\pi/6}^{\pi/3} \left( \frac{1+\sqrt{\tan x}}{1+\sqrt{\tan x}} \right) dx$

$2I = \int_{\pi/6}^{\pi/3} 1 \cdot dx$

Step 4: Solve the integral.
$2I = [x]_{\pi/6}^{\pi/3}$

$2I = \frac{\pi}{3} - \frac{\pi}{6}$

$2I = \frac{\pi}{6}$

$I = \frac{\pi}{12}$

Correct Option: (c)

Q6: If m and n are the order and degree, respectively of the differential equation $y{(\frac{dy}{dx})}^{3}+x^{3}(\frac{d^{2}y}{dx^{2}})^{2}-xy=sin~x,$ then write the value of $m+n$ .

(a) 1

(b) 2

(d) 4

Solution: We need to identify the Order (m) and Degree (n) of the given differential equation.
Step 1: Identify the Order (m).
The order of a differential equation is the order of the highest derivative present.
In the equation $y{(\frac{dy}{dx})}^{3}+x^{3}(\frac{d^{2}y}{dx^{2}})^{2}-xy=sin~x$ :

First derivative: $\frac{dy}{dx}$

Second derivative: $\frac{d^{2}y}{dx^{2}}$

The highest derivative is 2. So, $m = 2$ .

Step 2: Identify the Degree (n).
The degree is the power of the highest order derivative when the equation is a polynomial in derivatives.
The highest order derivative is $\frac{d^{2}y}{dx^{2}}$ .

The power raised to this term is 2.
So, $n = 2$ .

Step 3: Calculate m + n.
$m+n = 2+2 = 4$

Correct Option: (d)

Q7: The magnitude of each of the two vectors $\vec{a}$ and $\vec{b}$ , having the same magnitude such that the angle between them is $60^{\circ}$ and their scalar product is $9/2$ is:

(a) 2

(b) 3

(d) 5

Solution:
Step 1: Write the Dot Product formula.
$\vec{a} \cdot \vec{b} = |\vec{a}| |\vec{a}| \cos \theta$

Step 2: Substitute the known values.
$\vec{a} \cdot \vec{b} = \frac{9}{2}$
$\theta = 60^{\circ}$

Let $|\vec{a}| = |\vec{b}| = x$
$\frac{9}{2} = x \cdot x \cdot \cos 60^{\circ}$

Step 3: Solve for x.
$\frac{9}{2} = x \cdot x \cdot \frac{1}{2}$

Multiply both sides by 2:
$9 = x^2$
$x = 3$ (Magnitude cannot be negative)

Correct Option: (b)

Q8: Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let $F=4x+6y$ be the objective function. The minimum value of F occurs at:

(a) Only (0, 2)

(b) Only (3, 0)

(d) any point on the line segment joining the points (0, 2) and (3, 0)

Solution:
To find where the minimum value occurs, we must evaluate the objective function $F = 4x + 6y$ at each corner point.

Step 1: Evaluate F at each corner point.

At (0, 2): $F = 4(0) + 6(2) = 12$
At (3, 0): $F = 4(3) + 6(0) = 12$
At (6, 0): $F = 4(6) + 6(0) = 24$
At (6, 8): $F = 4(6) + 6(8) = 24 + 48 = 72$
At (0, 5): $F = 4(0) + 6(5) = 30$

Step 2: Identify the minimum value.
The minimum value is 12. It occurs at two distinct corner points: (0, 2) and (3, 0).

Step 3: Apply LPP Property.
If the optimal value (minimum or maximum) of an objective function occurs at two adjacent corner points, it occurs at every point on the line segment joining these two points.

Minimum value occurs any point on the line segment joining the points (0, 2) and (3, 0)

Correct Option: (d)

Q9: If a line makes angles $\alpha, \beta, \gamma$ with the positive direction of co-ordinates axes, then find the value of $sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma$ .

(a) 1

(b) 2

(d) 4

Solution: The angles $\alpha, \beta, \gamma$ are the direction angles.
The cosines of these angles ( $\cos\alpha, \cos\beta, \cos\gamma$ ) are the Direction Cosines (l, m, n).

Step 1: Use the property of Direction Cosines.
We know the sum of the squares of the direction cosines is always 1.
$\cos^2 \alpha + \cos^2 \beta + \cos\gamma = 1$

Step 2: Convert Cosine to Sine.
Using the identity $\cos^2\theta = 1 - \sin^2\theta$ :

$(1 - \sin^2\alpha) + (1 - \sin^2\beta) + (1 - \sin^2\gamma) = 1$

Step 3: Simplify the equation.
$1 + 1 + 1 - (\sin^2\alpha + \sin^2\beta + \sin^2\gamma) = 1$

$3 - (\sin^2\alpha + \sin^2\beta + \sin^2\gamma) = 1$

$3 - 1 = \sin^2\alpha + \sin^2\beta + \sin^2\gamma$

$\sin^2\alpha + \sin^2\beta + \sin^2\gamma = 2$

Correct Option: (b)

Q10: The projection of the vector $2\hat{i}+3\hat{j}+2\hat{k}$ on the vector $\hat{i}+2\hat{j}+\hat{k}$ is

(a) $10/\sqrt{6}$

(b) $10/\sqrt{3}$

(d) $5/\sqrt{3}$

Solution: The projection of a vector $\vec{a}$ on vector $\vec{b}$ is given by the formula:
$\text{Projection } = \frac{\vec{a} \cdot \vec{b}} {|\vec{b}| }$

Step 1: Identify the vectors.
Let $\vec{a} = 2\hat{i} + 3\hat{j} + 2\hat{k}$
Let $\vec{b} = \hat{i} + 2\hat{j} + \hat{k}$

Step 2: Calculate the dot product ( $\vec{a} \cdot \vec{b}$ ).
$\vec{a} \cdot \vec{b} = (2)(1) + (3)(2) + (2)(1)$
$\vec{a} \cdot \vec{b} = 2 + 6 + 2 = 10$

Step 3: Calculate the magnitude of $\vec{b}$ ( $|\vec{b}|$ ).
$|\vec{b}| = \sqrt{1^2 + 2^2 + 1^2}$
$|\vec{b}| = \sqrt{1 + 4 + 1} = \sqrt{6}$

Step 4: Calculate the projection.
$\text{Projection } = \frac{10} {\sqrt{6}}$

Correct Option: (a)

Q11: The number of arbitrary constants in the particular solution of a differential equation of third order are

(a) 3

(b) 2

(d) 0

Solution: We need to distinguish between a General Solution and a Particular Solution.
Step 1: Understanding the definitions.

General Solution: Contains arbitrary constants equal to the order of the differential equation. For a 3rd order differential equation, the general solution has 3 arbitrary constants.
Particular Solution: Obtained from the general solution by assigning specific values to the arbitrary constants based on given conditions. Therefore, it contains no arbitrary constants.

Step 2: Answering ths question.
The question asks for the number of arbitrary constants in the particular solution. Number of arbitrary constants = 0.

Correct Option: (d)

Q12: The value of $\int_{1}^{2}\frac{dx}{x\sqrt{x^{2}-1}}$ is

(a) $\pi/3$

(b) $\pi/2$

(d) $\pi/6$

Solution:
Step 1: Identify the standard integral.
We know that $\int \frac{dx}{x\sqrt{x^2 - a^2}} = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C$ .

Here, $a = 1$ .
So, $\int \frac{dx}{x\sqrt{x^2 - 1}} = \sec^{-1}x$ .

Step 2: Apply the limits.
$I = = [\sec^{-1}x]_{1}^{2}$ .

$I = \sec^{-1}(2) - \sec^{-1}(1)$

Step 3: Evaluate the trigonometric values.
$\sec^{-1}(2) = \frac{\pi}{3}$

$\sec^{-1}(1) = 0$

$I = \frac{\pi}{3} - 0 = \frac{\pi}{3}$

Correct Option: (a)

Q13: If $x\begin{bmatrix} 2 \\ 3 \end{bmatrix} + y\begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix}$ , find the value of x.

(a) 1

(b) 2

(d) 4

Solution:
Step 1: Form the equations. Multiply the scalars into the matrices:
$\begin{bmatrix} 2x \\ 3x \end{bmatrix} + \begin{bmatrix} -y \\ y \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix}$

$\begin{bmatrix} 2x - y \\ 3x + y \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix}$

Equating the corresponding elements:
$2x - y = 10$ … (i)
$3x + y = 5$ … (ii)

Step 2: Solve for x. Add equation (i) and equation (ii) to eliminate $y$ :
$(2x - y) + (3x + y) = 10 + 5$
$5x = 15$
$x = 3$

Correct Option: (c)

Q14: Feasible region (shaded) for a LPP is shown in the given figure. The maximum value of the $Z=0.4x+y$ is

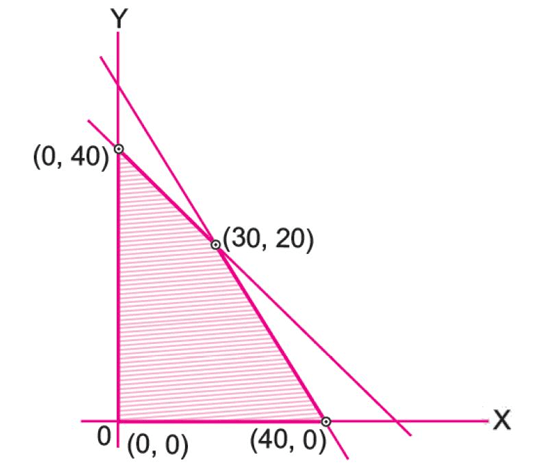
(a) 45

(b) 40

(d) 41

Solution:
The maximum value of the objective function $Z$ in a Linear Programming Problem occurs at one of the corner points of the feasible region.
Based on the provided figure description/coordinates, the corner points are: A(0, 0), B(40, 0), C(30, 20), and D(0, 40).

Step 1: Evaluate Z at each corner point. Objective Function: $Z = 0.4x + y$

At (0, 0): $Z = 0.4(0) + 0 = 0$
At (40, 0): $Z = 0.4(40) + 0 = 16$
At (30, 20): $Z = 0.4(30) + 20 = 12 + 20 = 32$
At (0, 40): $Z = 0.4(0) + 40 = 40$

Step 2: Identify the maximum value. The calculated values are 0, 16, 32, and 40. The maximum value is 40.
Correct Option: (b)

Q15: If $\begin{vmatrix} 2x+5 & 3 \\ 5x+2 & 9 \end{vmatrix} = 0$ , find x.

(a) 13

(b) 3

(d) $\sqrt{3}$

Solution:
Expanding the determinant.
$(2x+5)(9) - (3)(5x+2) = 0$
$(18x+45) - (15x+6) = 0$
$18x - 15x + 45 - 6 = 0$
$3x + 39 = 0$
$3x = -39$
$x = -13$

Correct Option: (c)

Q16: If A is a non-singular matrix of order 3 and $|A|=-4$ , find $|adj A|$ .

(a) 4

(b) 16

(d) $\frac{1}{4}$

Solution:
Using Formula
$|adj A| = |A|^{n-1}$
Where $n$ is the order of the matrix.

Substituting the values.
Here, $n = 3$ and $|A| = -4$ .

$|adj A| = (-4)^{3-1}$

$|adj A| = (-4)^{2}$

$|adj A| = 16$

Correct Option: (b)

Q17: The straight line $\frac{x-3}{3}=\frac{y-2}{1}=\frac{z-1}{0}$ is:

(a) parallel to x-axis

(b) parallel to y-axis

(d) perpendicular to z-axis

Solution: We determine the orientation of the line from its direction ratios.
Step 1: Identify direction ratios.
The direction ratios of the line are proportional to the denominators: $\vec{d} = (3, 1, 0)$ .

Step 2: Analyze the z-component.
The z-component of the direction vector is 0.
This means there is no change in the z-coordinate as you move along the line.
Therefore, the line lies in a plane parallel to the XY-plane (specifically the plane $z = 1$ ).

Step 3: Relate to the axes.
The Z-axis is perpendicular to the XY-plane.
Since the line is parallel to the XY-plane, it is perpendicular to the Z-axis.

Alternatively, the dot product of the line’s direction $(3, 1, 0)$ and the Z-axis direction $(0, 0, 1)$ is:
$3(0) + 1(0) + 0(1) = 0$
Since the dot product is 0, the line is perpendicular to the Z-axis.

Correct Option: (d)

Q18: If $|\vec{a}|=10$ , $|\vec{b}|=2$ and $\vec{a} \cdot \vec{b}=12$ , then the value of $|\vec{a} \times \vec{b}|$ is

(a) 5

(b) 10

(d) 16

Solution:
We use Lagrange’s Identity relating dot product and cross product.
$|\vec{a} \times \vec{b} |^2 + (\vec{a} \cdot \vec{b})^2 = |\vec{a}|^2|\vec{b}|^2$

Let $X = |\vec{a} \times \vec{b}|$ .

$X^2 + (12)^2 = (10)^2 (2)^2$

$X^2 + 144 = 100 \times 4$

$X^2 + 144 = 400$

$X^2 = 400 -144$

$X^2 = 256$

$X = \sqrt{256}$
$X = 16$

Correct Option: (d)

Q19: Assertion (A): The angle between the straight lines $\frac{x-1}{1}=\frac{y+2}{2}=\frac{z-3}{-3}$ and $\frac{x+1}{2}=\frac{y-2}{5}=\frac{z+3}{4}$ is $90^{\circ}$ .

Reason (R): Skew lines are lines in different planes which are parallel and intersecting.

Solution:
Check Assertion (A). To find the angle between two lines, we check the dot product of their direction ratios. If the dot product is zero, the lines are perpendicular (angle is $90^{\circ}$ ).
Direction ratios of Line 1 ( $\vec{d_1}$ ): $<1, 2, -3>$
Direction ratios of Line 2 ( $\vec{d_2}$ ): $<2, 5, 4>$

Calculate the dot product $\vec{d_1} \cdot \vec{d_2}$ :
$\vec{d_1} \cdot \vec{d_2} = (1)(2) + (2)(5) + (-3)(4)$
$\vec{d_1} \cdot \vec{d_2} = 2 + 10 - 12 = 0$

Since the dot product is 0, the lines are perpendicular. Therefore, Assertion (A) is True.

Check Reason (R). The statement says “Skew lines are lines in different planes which are parallel and intersecting.” By definition, Skew lines are lines in space that are neither parallel nor intersecting. They lie in different planes. Therefore, the statement “parallel and intersecting” makes this false. Reason (R) is False.

Conclusion. Assertion is True, but Reason is False. This corresponds to option (c).

Correct Option: (c)

Q20: Assertion (A): Domain of $f(x)=sin^{-1}x+cos~x$ is $[-1,1]$ .

Reason (R): Domain of a function is the set of all possible values for which function will be defined.

Solution:
Check Assertion (A). We need to find the domain of $f(x) = \sin^{-1}x + \cos x$ .

The domain of $\sin^{-1}x$ is $[-1, 1]$ .
The domain of $\cos x$ is $R$ (all real numbers).

The domain of the sum of two functions is the intersection of their individual domains.
Domain = $[-1, 1] \cap R$ Domain = $[-1, 1]$ Therefore, Assertion (A) is True.

Check Reason (R). The statement “Domain of a function is the set of all possible values for which function will be defined” is the standard definition of the domain. Therefore, Reason (R) is True.

Determine the relationship. The Reason correctly defines what a domain is. To determine if the Assertion is true, we must apply the definition given in the Reason.
Therefore, the Reason is the correct explanation for how we derived the Assertion.
Both A and R are true, and R is the correct explanation of A.
This corresponds to option (a).

Correct Option: (a)

Here are the step-by-step solutions for Section B (Questions 21 to 25), formatted for your WordPress Gutenberg Editor.

Section B: 2 Marks Questions

Q21: If $y=log(cos~e^{x})$ , then find $\frac{dy}{dx}$ .

Solution:
Step 1: Differentiate using chain rule
Let $u = \cos(e^x)$ .
Then $y = \log(u)$ .

$\frac{dy}{dx} = \frac{1}{u} \cdot \frac{du}{dx}$

$\frac{dy}{dx} = \frac{1}{\cos(e^x)} \cdot \frac{d}{dx}(\cos(e^x))$

Step 2: Differentiate the cosine function.
Let $v = e^x$ . Then $u = \cos(v)$ .
$\frac{d}{dx} (\cos(e^x)) = -\sin(e^x) \cdot \frac{d}{dx} (e^x)$

Step 3: Differentiate the exponential function.
$\frac{d}{dx} (e^x) = e^x$

Step 4: Combine all parts.
$\frac{dy}{dx} = \frac{1}{\cos(e^x)} \cdot \frac{d}{dx}(\cos(e^x))$

$\frac{dy}{dx} = \frac{1}{\cos(e^x)} \cdot (-\sin(e^x) \cdot \frac{d}{dx} (e^x))$

$\frac{dy}{dx} = \frac{1}{\cos(e^x)} \cdot [-\sin(e^x)] \cdot e^x$

$\frac{dy}{dx} = -e^x \cdot \frac{\sin(e^x)}{\cos(e^x)}$

$\frac{dy}{dx} = -e^x \cdot \tan(e^x)$

Q22: (A) Prove that the Greatest Integer Function $f:R\rightarrow R$ given by $f(x)=[x]$ is neither one-one nor onto.
Where $[x]$ denotes the greatest integer less than or equal to x.

Solution:
Step 1: Check for One-One (Injective).
A function is one-one if $f(x_1) = f(x_2) \implies x_1 = x_2$ .

Let us take two specific examples: $x_1 = 1.2$ and $x_2 = 1.9$ .
$f(1.2) = [1.2] = 1$
$f(1.9) = [1.9] = 1$

Here, $f(1.2) = f(1.9) = 1$ , but $1.2 \ne 1.9$ .
Therefore, different elements in the domain have the same image.
Hence, f is not one-one.

Step 2: Check for Onto (Surjective).
A function is onto if the Range is equal to the Codomain.

Codomain: The set of Real Numbers ( $R$ ).
Range: The output of $[x]$ is always an Integer ( $Z$ ).
For example, consider $0.7 \in R$ (Codomain).
There is no $x$ such that $[x] = 0.7$ because $[x]$ must be an integer.
Since Range ( $Z$ ) $\ne$ Codomain ( $R$ ), f is not onto.

Conclusion: The function is neither one-one nor onto.

Q22: (B) If $sin(sin^{-1}\frac{1}{5}+cos^{-1}x)=1,$ then find the value of x.

Solution:
$sin^{-1}\frac{1}{5}+cos^{-1}x=\sin^{-1}1$

So, $\sin^{-1}\frac{1}{5} + \cos^{-1}x = \frac{\pi}{2}$ … (1)

Use the Inverse Trigonometric Identity. We know the identity: $\sin^{-1}x + \cos^{-1}x = \frac{\pi}{2}$ .
Comparing the equation (1) with this identity:
$\sin^{-1}\frac{1}{5} + \cos^{-1}x = \sin^{-1}x + \cos^{-1}x$

$\sin^{-1}\frac{1}{5} = \sin^{-1}x$

$x = \frac{1}{5}$

Final Answer: $\boxed{x = \frac{1}{5}}$

Q23: If $|\vec{a}\times\vec{b}|^{2}+(\vec{a}.\vec{b})^{2}=144$ and $|\vec{a}|=4$ , then find the value of $|\vec{b}|$ .

Solution:
Step 1: We use Lagrange’s Identity for vectors.
$|\vec{a} \times \vec{b}|^2 + (\vec{a} \cdot \vec{b})^2 = |\vec{a}|^2 |\vec{b}|^2$

Step 2: Substituting the given values.
Given :LHS Sum = 144 and $|\vec{a}| = 4$ .

$144 = (4)^2 |\vec{b}|^2$
$144 = 16 |\vec{b}|^2$

Step 3: Solve for $|\vec{b}|$ .
$|\vec{b}|^2 = \frac{144}{16}$
$|\vec{b}|^2 = 9$
$|\vec{b}| = 3$

Final Answer: $\boxed{ |\vec{b}| = 3 }$

Q24: (A) A pair of dice is thrown. Find the probability of getting 7 as the sum, if it is known that the second die always exhibits an odd number.

Solution:
Let $A$ be the event of getting a sum of 7.
Let $B$ be the event that the second die shows an odd number.

We need to find the conditional probability $P(A|B)$ .

Step 1: Find the sample space for B.
The second die shows an odd number (1, 3, 5).
$B = \{ (1,1), (2,1), (3,1), (4,1), (5,1), (6,1),$
$(1,3), (2,3), (3,3), (4,3), (5,3), (6,3),$
$(1,5), (2,5), (3,5), (4,5), (5,5), (6,5) \}$

Total outcomes in B, $n(B) = 18$ .

Step 2: Find the intersection $A \cap B$ .
We need outcomes where the sum is 7 AND the second die is odd.
Pairs summing to 7 are: $(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)$ .

From these, select those where the second number is odd:
$A \cap B = { (2,5), (4,3), (6,1) }$
Number of outcomes, $n(A \cap B) = 3$ .

$P(A|B) = \frac{n(A \cap B)}{n(B)}$

Step 3: Calculate Probability.
$P(A|B) = \frac{3}{18} = \frac{1}{6}$

Final Answer: $\boxed {P(A|B) = \frac{1}{6} }$

Q24: (B) A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event ‘number is even’ and B be the event ‘number is marked red’. Find whether the events A and B are independent or not.

Solution:
Sample Space $S = {1, 2, 3, 4, 5, 6}$ . Total = 6.

Step 1: Calculate P(A).
Event A (Even): ${2, 4, 6}$ .
$P(A) = \frac{3}{6} = \frac{1}{2}$

Step 2: Calculate P(B).
Event B (Red): ${1, 2, 3}$ .
$P(B) = \frac{3}{6} = \frac{1}{2}$

Step 3: Calculate $P(A \cap B)$ .
Event $A \cap B$ (Even AND Red): The only even number in the red set {1, 2, 3} is 2.
$A \cap B = {2}$
$P(A \cap B) = \frac{1}{6}$

Step 4: Check Condition for Independence.
For independent events, $P(A \cap B)$ must equal $P(A) \times P(B)$ .
$P(A) \times P(B) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$

Since $\frac{1}{6} \ne \frac{1}{4}$ ,
i.e., $P(A \cap B) \ne P(A) \cdot P(B)$ .

Final Answer: The events A and B are not independent.

Q25: If $xy=log~y+C$ , then show that $\frac{dy}{dx}=\frac{y^{2}}{1-xy}$ .

Solution: We differentiate the given implicit equation with respect to $x$ .

Differentiate both sides.
$\frac{d}{dx}(xy) = \frac{d}{dx}(\log y) + \frac{d}{dx}(C)$

Using Product Rule on LHS and Chain Rule on RHS:
$x \cdot \frac{dy}{dx} + y \cdot (1) = \frac{1}{y} \cdot \frac{dy}{dx}$

Group terms involving $\frac{dy}{dx}$ .
$x \cdot \frac{dy}{dx} - \frac{1}{y} \cdot \frac{dy}{dx} = - y$

Factor out $\frac{dy}{dx}$ :
$\frac{dy}{dx} \left( x - \frac{1}{y} \right) = - y$

Simplify the term in brackets.
$\frac{dy}{dx} \left( \frac{xy - 1}{y} \right) = - y$

$\frac{dy}{dx} =\frac{-y \cdot y}{xy - 1}$

$\frac{dy}{dx} = \frac{-y^2}{xy - 1}$

$\frac{dy}{dx} = \frac{y^2}{1-xy}$

Hence Proved

Section C: 3 Marks Questions

Q26: The scalar product of the vector $\vec{a}=\hat{i}+\hat{j}+\hat{k}$ with a unit vector along the sum of the vectors $\vec{b}=2\hat{i}+4\hat{j}-5\hat{k}$ and $\vec{c}=\mu\hat{i}+2\hat{j}+3\hat{k}$ is equal to one. Find the value of $\mu$ and hence find the unit vector along $\vec{b}+\vec{c}$ .

Solution:
Step 1: Find the sum vector
$\vec{r} = \vec{b} + \vec{c}$ .
$\vec{r} = (2\hat{i}+4\hat{j}-5\hat{k}) + (\mu\hat{i}+2\hat{j}+3\hat{k})$
$\vec{r} = (2+\mu)\hat{i} + (4+2)\hat{j} + (-5+3)\hat{k}$
$\vec{r} = (2+\mu)\hat{i} + 6\hat{j} - 2\hat{k}$

Step 2: Find the unit vector along $\vec{r}$ .
Let $\hat{r}$ be the unit vector along $\vec{r}$ .
$\hat{r} = \frac{\vec{r}}{|\vec{r}|} = \frac{(2+\mu)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{(2+\mu)^2 + 6^2 + (-2)^2}}$

$\hat{r} = \frac{(2+\mu)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{(2+\mu)^2 + 40}}$

Step 3: Use the Scalar Product condition.
Given that $\vec{a} \cdot \hat{n} = 1$ .
$(\hat{i}+\hat{j}+\hat{k}) \cdot \left( \frac{(2+\mu)\hat{i} + 6\hat{j} - 2\hat{k}}{\sqrt{(2+\mu)^2 + 40}} \right) = 1$

$\frac{1(2+\mu)\hat{i} + 1(6)\hat{j} +1(-2)\hat{k}}{\sqrt{(2+\mu)^2 + 40}} = 1$

$\frac{\mu + 6}{\sqrt{\mu^2 + 4\mu + 4 + 40}} = 1$

$\mu + 6 = \sqrt{\mu^2 + 4\mu + 44}$

Step 4: Solve for $\mu$ .
Squaring both sides:
$(\mu + 6)^2 = \mu^2 + 4\mu + 44$

$\mu^2 + 12\mu + 36 = \mu^2 + 4\mu + 44$

$12\mu - 4\mu = 44 -36$

$8\mu = 8$

$\mu = 1$

Step 5: Find the unit vector.
Substitute $\mu = 1$ into the expression for $\hat{n}$ (from Step 2).

$\vec{r} = (2+1) \hat{i} + 6\hat{j} - 2\hat{k} = 3\hat{i} + 6\hat{j} - 2\hat{k}$

Magnitude $|\vec{r}| = \sqrt{3^2 + 6^2 + (-2)^2} = \sqrt{9+36+4} = \sqrt{49} = 7$
$\hat{r} = \frac{3\hat{i} + 6\hat{j} - 2\hat{k}}{7}$
$\hat{r} = \frac{3}{7}\hat{i} + \frac{6}{7}\hat{j} - \frac{2}{7}\hat{k}$

Final Answer: $\boxed{ \text{Value of } \mu = 1 }$ $\boxed{\text{Unit vector is } \frac{3}{7}\hat{i} + \frac{6}{7}\hat{j} - \frac{2}{7}\hat{k}}$ .

Q26: Find the points on the line $\frac{(x+2)}{3}=\frac{(y+1)}{2}=\frac{(z-3)}{2}$ at a distance of $3\sqrt{2}$ units from the point $P(1,2,3)$ .

Solution:
Step 1: Express a general point on the line.
Let the given line be equal to $\lambda$ .
$\frac{(x+2)}{3}=\frac{(y+1)}{2}=\frac{(z-3)}{2} = \lambda$

Any point $Q$ on the line can be written as:
$Q(3\lambda - 2, 2\lambda - 1, 2\lambda + 3)$

Step 2: Use the distance formula.
We are given that the distance $PQ = 3\sqrt{2}$ .
$P = (1, 2, 3)$

$PQ^2 = (3\sqrt{2})^2 = 18$
Using the distance formula $(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2$ :
$(3\lambda - 2 -1)^2 + (2\lambda - 1 - 2)^2 + (2\lambda + 3 - 3)^2) = 18$
$(3\lambda - 3)^2 + (2\lambda - 3)^2 + (2\lambda)^2 = 18$

Step 3: Solve for $\lambda$ .
Expand the squares:
$9(\lambda - 1)^2 + (4\lambda^2 - 12\lambda + 9) + 4\lambda^2 = 18$
$9(\lambda^2 - 2\lambda + 1) + 4\lambda^2 - 12\lambda + 9 + 4\lambda^2 = 18$
$9\lambda^2 - 18\lambda + 9 + 4\lambda^2 - 12\lambda + 9 + 4\lambda^2 = 18$
$17\lambda^2 - 30\lambda + 18 = 18$
$17\lambda^2 - 30\lambda = 0$
$\lambda(17\lambda - 30) = 0$

So, $\lambda = 0$ or $\lambda = \frac{30}{17}$ .

Step 4: Find the coordinates of the points.
Case 1: When $\lambda = 0$ :
$Q(3(0) - 2, 2(0) - 1, 2(0) + 3)$
$Q = (-2, -1, 3)$

Case 2: When $\lambda = \frac{30}{17}$ :
$x = 3(\frac{30}{17}) - 2 = \frac{90 - 34}{17} = \frac{56}{17}$

$y = 2(\frac{30}{17}) - 1 = \frac{60-17}{17} = \frac{43}{17}$

$y = 2(\frac{30}{17}) + 3 = \frac{60+51}{17} = \frac{111}{17}$

$Q = (\frac{56}{17}, \frac{43}{17}, \frac{111}{17})$

Final Answer: The points are $\boxed{ (-2, -1, 3) \text{ and } (\frac{56}{17}, \frac{43}{17}, \frac{111}{17}) }$ .

Q27: Evaluate: $\int\frac{x^{2}+1}{(x^{2}+2)(x^{2}+3)}dx$

Solution:
Step 1: Partial Fraction Decomposition.
Let $x^2 = t$ for the purpose of partial fractions (Note: Do not differentiate, just substitute for algebraic simplification).
$\frac{t+1}{(t+2)(t+3)} = \frac{A}{t+2} + \frac{B}{t+3}$

$t + 1 = A(t+3) + B(t+2)$

Find A and B:
Put $t = -2$ :
$-2 + 1 = A(-2+3) + B(0) \implies -1 = A \implies A = -1$

Put $t = -3$ :
$-3 + 1 = A(0) + B(-3+2) \implies -2 = -B \implies B = 2$

Substituting back into the expression:
$\frac{t+1}{(t+2)(t+3)} = \frac{-1}{t+2} + \frac{2}{t+3}$

$\frac{x^2+1}{(x^2+2)(x^2+3)} = \frac{-1}{x^2+2} + \frac{2}{x^2+3}$

Step 2: Evaluate the Integral.
$I = \int \left( \frac{-1}{x^2+(\sqrt{2})^2} + \frac{2}{x^2+(\sqrt{3})^2} \right) \ dx$

Using the standard formula: $\int \frac{dx}{x^2+a^2} = \frac{1}{a}\tan^{-1}(\frac{x}{a})$

$I = -1 \cdot \frac{1}{\sqrt{2}}\tan^{-1}\left(\frac{x}{\sqrt{2}}\right) + 2 \cdot \frac{1}{\sqrt{3}}\tan^{-1}\left(\frac{x}{\sqrt{3}}\right) + C$

Final Answer: $\boxed{ I = \frac{2}{\sqrt{3}}\tan^{-1}\left(\frac{x}{\sqrt{3}}\right) - \frac{1}{\sqrt{2}}\tan^{-1}\left(\frac{x}{\sqrt{2}}\right) + C }$

Q28: (A) Evaluate: $\int_{0}^{\pi}\frac{x~sin~x}{1+cos^{2}x}dx$

Solution:
Step 1: Apply Property $P_4$ .
Let $I = \int_{0}^{\pi}\frac{x \sin x}{1+\cos^{2}x}dx$ … (i)

Property: $\int_{0}^{a}f(x)dx = \int_{0}^{a}f(a-x)dx$

Let $I = \int_{0}^{\pi}\frac{(\pi - x) \sin (\pi - x)}{1+\cos^{2}(\pi - x)}dx$

Since $\sin(\pi-x) = \sin x$ and $\cos(\pi-x) = -\cos x$ (so $\cos^2$ remains positive):
$I = \int_{0}^{\pi}\frac{(\pi-x) \sin x}{1+\cos^{2}x}dx$ … (ii)

Step 2: Add equations (i) and (ii).
$2I = \int_{0}^{\pi}\frac{x \sin x + (\pi-x) \sin x}{1+\cos^{2}x}dx$

$2I = \int_{0}^{\pi} \frac{\pi \sin x}{1+\cos^{2}x} dx$

$2I = \pi \int_{0}^{\pi} \frac{\sin x}{1+\cos^{2}x} dx$

Step 3: Integration by Substitution.
Let $\cos x = t$ .
Then $-\sin x dx = dt \implies \sin x dx = -dt$ .
Limits: When $x = 0, t = 1$ . When $x = \pi, t = -1$ .

$2I = \pi \int_{1}^{-1} \frac{-dt}{1+t^2}$

$2I = \pi \int_{-1}^{1} \frac{dt}{1+t^2}$ (Swapping limits removes the negative sign)

Since the integrand $\frac{1}{1+t^2}$ is an even function:
$2I = \pi \cdot 2 \int_{0}^{1} \frac{dt}{1+t^2}$

$I = \pi \int_{0}^{1} \frac{dt}{1+t^2}$

Step 4: Final Evaluation.
$I = \pi [\tan^{-1} t]_{0}^{1}$

$I = \pi (\tan^{-1}(1) - \tan^{-1}(0))$

$I = \pi (\frac{\pi}{4} - 0)$

$I = \frac{\pi^2}{4}$

Final Answer: $\boxed{ \int_{0}^{\pi}\frac{x~sin~x}{1+cos^{2}x}dx = \frac{\pi^2}{4} }$

Q28: (B) Evaluate: $\int_{1}^{3}|x^{2}-2x|dx$

Solution:

Step 1: Analyze the Modulus Function.
$f(x) = x^2 - 2x = x(x-2)$ .
The critical points are where $x(x-2) = 0$ , which are $x = 0$ and $x = 2$ .
We are integrating from $x=1$ to $x=3$ .

In the interval $[1, 2]$ : Take $x = 1.5$ . $1.5(1.5-2) < 0$ . So $x^2-2x$ is negative. $|x^2-2x| = -(x^2-2x) = 2x - x^2$ .
In the interval $[2, 3]$ : Take $x = 2.5$ . $2.5(2.5-2) > 0$ . So $x^2-2x$ is positive. $|x^2-2x| = x^2 - 2x$ .

Step 2: Split the Integral.
$I = \int_{1}^{2} (2x - x^{2}) dx + \int_{2}^{3} (x^{2}-2x) dx$

Step 3: Evaluate the Integrals.
Part 1: $\ \left[ \frac{2x^2}{2} - \frac{x^3}{3} \right]_{1}^{2}$

$\ \left[ x^2 - \frac{x^3}{3} \right]_{1}^{2}$

Upper limit (2): $4 - \frac{8}{3} = \frac{4}{3}$

Lower limit (1): $1 - \frac{1}{3} = \frac{2}{3}$

Part 1: $\frac{4}{3} - \frac{2}{3} = \frac{2}{3}$

Part 2: $\left[ \frac{x^3}{3} - x^2 \right]_{2}^{3}$

Upper limit (3): $\frac{27}{3} - 9 = 9 - 9 = 0$

Lower limit (2): $\frac{8}{3} - 4 = \frac{8-12}{3} = \frac{-4}{3}$

Part 2: $0 - (\frac{-4}{3}) = \frac{4}{3}$

Step 4: Sum the results.
$I = \frac{2}{3} + \frac{4}{3} = \frac{6}{3} = 2$

Final Answer: $\boxed{ \int_{1}^{3}|x^{2}-2x|dx = 2}$

Q29: Find the general solution of the following differential equation: $(x^{2}-y^{2})dx+2xy~dy=0$ .

Solution:
Step 1: Rewrite the equation.
$(x^{2}-y^{2})dx+2xy~dy=0$
$2xy \ dy= -(x^{2}-y^{2}) \ dx$
$\frac{dy}{dx} = \frac{y^2 - x^2}{2xy}$

This is a homogeneous differential equation since the degree of both numerator and denominator is 2.

Step 2: Substitution.
Let $y = vx$ .
Then, differentiating with respect to x: $\frac{dy}{dx} = v + x\frac{dv}{dx}$ .

Substitute these into the equation:
$v + x\frac{dv}{dx} = \frac{(vx)^2 - x^2}{2x(vx)}$

$v + x\frac{dv}{dx} = \frac{x^2(v^2 - 1)}{2x^2v}$

$v + x\frac{dv}{dx} = \frac{v^2 - 1}{2v}$

Step 3: Separate Variables.
$x\frac{dv}{dx} = \frac{v^2 - 1}{2v} - v$

$x\frac{dv}{dx} = \frac{v^2 - 1 - 2v^2}{2v}$

$x\frac{dv}{dx} = \frac{-1(1 + v^2)}{2v}$

Rearrange to separate $v$ and $x$ :
$\frac{2v}{1 + v^2} dv = -\frac{dx}{x}$

Step 4: Integrate both sides.
$\int \frac{2v}{1 + v^2} dv = - \int \frac{dx}{x}$

For LHS, let $1+v^2 = t$ , then $2v dv = dt$ .
$\int \frac{dt}{t} = -\ln|x| + C$

$\ln|1 + v^2| = -\ln|x| + \ln|C|$ (Using $\ln C$ as the constant)

Step 5: Simplify.
$\ln|1 + v^2| = \ln \left| \frac{C}{x} \right|$

$1 + v^2 = \frac{C}{x}$

Substitute $v = \frac{y}{x}$ back:
$1 + \left(\frac{y}{x} \right)^2 = \frac{C}{x}$

$\frac{x^2 + y^2}{x^2} = \frac{C}{x}$

$x^2 + y^2 = Cx$

Final Answer: $\boxed{ x^2 + y^2 = Cx }$

Q29: (B) Solve: $x \log x \frac{dy}{dx} + y = \frac{2}{x} \log x$ .

Solution:
This is a Linear Differential Equation of the form $\frac{dy}{dx} + Py = Q$ .

Step 1: Standardize the equation.
Divide the entire equation by $x \log x$ to isolate $\frac{dy}{dx}$ :
$\frac{dy}{dx} + \frac{y}{ x \log x} = \frac{2 \log x} {x( x \log x)}$ .

$\frac{dy}{dx} + \left(\frac{1}{x \log x}\right)y = \frac{2}{x^2}$

Here: $P = \frac{1}{ x \log x}$

$Q = \frac{2}{x^2}$

Step 2: Find the Integrating Factor (IF).
$IF = e^{\int P dx} = e^{\int \frac{1}{x \log x} dx}$

Put $\log x = t \implies \frac{1}{x} dx = dt$ .
$\int \frac{1}{x \log x} dx = \int \frac{dt}{t} = \ln t = \ln(\log x)$

$IF = e^{\ln(\log x)} = \log x$

Step 3: Solution.
$y \cdot (IF) = \int (Q \cdot IF) dx + C$

$y \log x = \int \left( \frac{2}{x^2} \cdot \log x \right) dx + C$

Step 4: Integrate RHS.
Use Integration by Parts for $\int \frac{2 \log x}{x^2} dx$ .

Let $u = \log x$ and $v = \frac{2}{x^2}$ .

$\frac{du}{dx} = \frac{1}{x}$

$\int v dx = \int 2x^{-2} dx = \frac{2x^{-1}}{-1} = -\frac{2}{x}$

$\int u dv = u \int v dx - \int \frac{du}{dx} \int v dx$

$\int \frac{2 \log x}{x^2} dx = (\log x) (-\frac{2}{x}) - \int (-\frac{2}{x}) \cdot \frac{1}{x} dx$

$= -\frac{2 \log x}{x} + 2 \int x^{-2} dx$

$= -\frac{2 \log x}{x} + 2 \left( \frac{x^{-1}}{-1}\right)$

$= -\frac{2 \log x}{x} - \frac{2}{x}$

Final Solution. $\boxed{ y \log x = -\frac{2}{x}(\log x + 1) + C}$

Q30: Solve the following Linear Programming Problem graphically: Minimize $Z=13x-15y$ subject to the constraints $x+y\le7,$ $2x-3y+6\ge0$ , $x\ge0$ and $y\ge0$ .

Solution:
Step 1: Plot the constraint lines.

$x + y = 7$ : Passes through (0, 7) and (7, 0).
- Test point (0,0): $0 \le 7$ (True). Shade towards origin.
$2x - 3y = -6$ (Rewritten):
- If $x=0$ , $-3y = -6 \implies y = 2$ . Point (0, 2).
- If $y=0$ , $2x = -6 \implies x = -3$ . Point (-3, 0).
- Test point (0,0): $0 - 0 + 6 \ge 0$ (True). Shade towards origin (region containing 0,0).

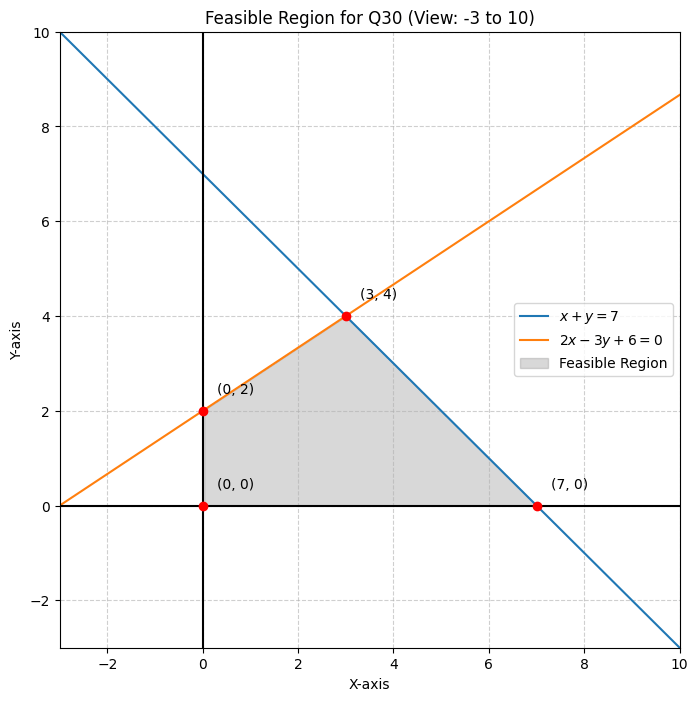
Step 2: Find the Feasible Region. The common region bounded by these lines and the first quadrant axes ( $x \ge 0, y \ge 0$ ) has the following corner points:

O (0,0): Intersection of axes.
A (0, 2): Intersection of $2x - 3y + 6 = 0$ with y-axis.
B (3, 4): Intersection of 2x - 3y + 6 = 0 and x + y = 7 .
- (Solve simultaneously: $3(x+y)=21$ + $2x-3y=-6$ $\implies 5x=15 \implies x=3, y=4$ )
C (7, 0): Intersection of $x + y = 7$ with x-axis.

Step 3: Evaluate Z at Corner Points. Objective Function: $Z = 13x - 15y$

At O (0, 0): $Z = 0$
At C (7, 0): $Z = 13(7) - 0 = 91$
At B (3, 4): $Z = 13(3) - 15(4) = 39 - 60 = -21$
At A (0, 2): $Z = 13(0) - 15(2) = -30$

Step 4: Determine Minimum. Comparing the values (0, 91, -21, -30), the minimum value is -30.

Final Answer: $\boxed{ \text{The minimum value of Z is } -30 \text { and it occurs at the point } (0, 2). }$

Q31: Evaluate: $\int e^{x}\frac{(1-sin~x)}{(1-cos~x)}dx$ .

Solution:
Step 1: Simplify the integrand using Trigonometric Identities.
We know:
$1 - \cos x = 2 \sin^2{\frac{x}{2}}$

$\sin x = 2 \sin(\frac{x}{2}) \cos(\frac{x}{2})$

Substitute these into the fraction:
$\frac{1 - \sin x}{1 - \cos x } = \frac{1 - 2 \sin(\frac{x}{2}) \cos(\frac{x}{2})}{2 \sin^2{\frac{x}{2}}}$

$\frac{1}{2 \sin^2{\frac{x}{2}}} - \frac{2 \sin(\frac{x}{2}) \cos(\frac{x}{2})}{2 \sin^2{\frac{x}{2}}}$

$I = \frac{1}{2}\cosec^2(x/2) - \cot(x/2)$

So the integral becomes:
$I = \int e^x \left[ - \cot(x/2) + \frac{1}{2}\cosec^2(x/2) \right] dx$

Step 3: Apply the Standard Form.
We know that $\int e^x [f(x) + f'(x)] dx = e^x f(x) + C$ .
Let $f(x) = -\cot(x/2)$ .
Differentiating using Chain Rule:
$f'(x) = -(-\cosec^2(x/2)) \cdot \frac{d}{dx}(x/2)$

$f'(x) = \cosec^2(x/2) \cdot \frac{1}{2}$

$f'(x) = \frac{1}{2} \cosec^2(x/2)$

This matches the second term in our bracket exactly.

Step 4: Write the Final Answer.
$I = e^x f(x) + C$
$I = -e^x \cot(x/2) + C$

Final Answer: $\boxed{ \int e^{x}\frac{(1-sin~x)}{(1-cos~x)}dx = -e^x \cot \left(\frac{x}{2} \right) + C }$

Section D: 5 Marks Questions

Q32: Show that each of the relation R in the set $A={x\in Z:0\le x\le12}$ , given by $R={(a,b):|a-b| \text{ is a multiple of 4}}$ is an equivalence relation. Find the set of all elements related to 1 in each case.

Solution:
Step 1: Check for Reflexivity.
For any element $a \in A$ , we check $(a, a) \in R$ .
$|a - a| = |0| = 0$ .
Since 0 is a multiple of 4 (as $0 = 4 \times 0$ ),
$(a, a) \in R$ . Therefore, R is Reflexive.

Step 2: Check for Symmetry.
Let $(a, b) \in R$ .
This means $|a - b|$ is a multiple of 4.
$|a - b| = 4k$ for some integer $k$ .

We know that $|b - a| = |-(a - b)| = |a - b|$ .
So, $|b - a| = 4k$ .
This implies $(b, a) \in R$ . Therefore, R is Symmetric.

Step 3: Check for Transitivity.
Let $(a, b) \in R$ and $(b, c) \in R$ .
$|a - b| = 4m$ and $|b - c| = 4n$ .
This implies $a - b = \pm 4m$ and $b - c = \pm 4n$ .

Adding these two equations:
$(a - b) + (b - c) = \pm 4m \pm 4n$
$a - c = 4(\pm m \pm n)$
Thus, $|a - c|$ is a multiple of 4.
So, $(a, c) \in R$ . Therefore, R is Transitive.

Conclusion: Since R is reflexive, symmetric, and transitive, it is an Equivalence Relation.

Step 4: Find elements related to 1.
We need to find $x \in A$ such that $(x, 1) \in R$ .
Condition: $|x - 1|$ is a multiple of 4.
Given $A = {0, 1, 2, ..., 12}$ .

If $|x - 1| = 0 \implies x = 1$
If $|x - 1| = 4 \implies x - 1 = 4 \text{ or } x - 1 = -4 \implies x = 5 \text{ (since -3 is not in A)}$
If $|x - 1| = 8 \implies x = 9$
If $|x - 1| = 12 \implies x = 13 \text{ (not in A)}$

The set of related elements is ${1, 5, 9}$ .

Q32 (Alternative): Let $A=R-{2}$ and $B=R-{1}$ . If $f:A\rightarrow B$ is a function defined by $f(x)=\frac{x-1}{x-2}$ , then show that f is one-one and onto.

Solution:
Step 1: Check for One-One (Injective).
Let $x_1, x_2 \in A$ such that $f(x_1) = f(x_2)$ .
$\frac{x_1 - 1}{x_1 - 2} = \frac{x_2 - 1}{x_2 -2}$

$\frac{x_1 - 1}{x_2 - 2} = \frac{x_2 - 1}{x_1 -2}$

$x_1 x_2 - 2x_1 - x_2 + 2 = x_1 x_2 - 2x_2 - x_1 + 2$

$- 2x_1 - x_2 = - 2x_2 - x_1$

$2x_2 - x_2 = 2x_1 - x_1$

$x_2 = x_1$ Therefore, f is One-One.

Step 2: Check for Onto (Surjective).
Let $y \in B$ (Codomain).
We need to find $x \in A$ such that $f(x) = y$ .
$y = \frac{x-1}{x-2}$

Cross multiply to solve for x:
$y(x-2) = x-1$
$xy - 2y = x - 1$
$xy - x = 2y -1$
$x(y - 1) = 2y - 1$
$x = \frac{2y - 1}{y - 1}$

Since $y \in R - {1}$ , the denominator $y - 1 \neq 0$ , so $x$ is defined.
We must also check if $x \neq 2$ (since Domain A is $R - {2}$ ).
If $\frac{2y - 1}{y - 1} = 2$ , then $2y - 1 = 2y - 2 \implies -1 = -2$ , which is impossible.

Thus, $x \in A$ for every $y \in B$ . Therefore, f is Onto.

Q33: Find the shortest distance between the lines $\vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+\lambda(\hat{i}+2\hat{j}+2\hat{k})$ and $\vec{r}=5\hat{i}-2\hat{j}+\mu(3\hat{i}+2\hat{j}+6\hat{k})$ . If the lines intersect find their point of intersection.

Solution:
Step 1: Identify coordinates and direction vectors.
Line 1: $\vec{a_1} = (3, 2, -4)$ , $\vec{b_1} = (1, 2, 2)$
Line 2: $\vec{a_2} = (5, -2, 0)$ , $\vec{b_2} = (3, 2, 6)$

Step 2: Calculate $\vec{a_2} - \vec{a_1}$ .
$\vec{a_2} - \vec{a_1} = (5-3) \hat{i} + (-2-2) \hat{j} + (0-(-4)) \hat{k}$
$\vec{a_2} - \vec{a_1} = 2\hat{i} - 4\hat{j} + 4\hat{k}$

Step 3: Calculate Cross Product $\vec{b_1} \times \vec{b_2}$ .
$\vec{b_1} \times \vec{b_2} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 2 \\ 3 & 2 & 6 \end{vmatrix}$

$= \hat{i}(12 - 4) - \hat{j}(6 - 6) + \hat{k}(2 - 6)$

$= 8\hat{i} - 0\hat{j} - 4\hat{k}$

Magnitude: $|\vec{b_1} \times \vec{b_2}| = \sqrt{8^2 + (-4)^2} = \sqrt{64 + 16} = \sqrt{80} = 4\sqrt{5}$

Step 4: Calculate Shortest Distance (SD).
$SD = \left| \frac{(\vec{b_1} \times \vec{b_2}) \cdot (\vec{a_2} - \vec{a_1})}{|\vec{b_1} \times \vec{b_2} |} \right|$
Numerator Dot Product: $(8\hat{i} - 4\hat{k}) \cdot (2\hat{i} - 4\hat{j} + 4\hat{k})$
$= 8(2) + 0(-4) + (-4)(4) = 16 -16 = 0$

Since the Shortest Distance is 0, the lines intersect.

Step 5: Find the Point of Intersection.
Equate position vectors:
$3 + \lambda = 5 + 3\mu \implies \lambda - 3\mu = 2$ … (i)
$2 + 2\lambda = -2 + 2\mu \implies 2\lambda - 2\mu = -4 \implies \lambda - \mu = -2$ … (ii)
$-4 + 2\lambda = 6\mu \implies \lambda - 3\mu = 2$ … (iii)

Solving (i) and (ii):
$(\lambda - 3\mu) - (\lambda - \mu) = 2 - (-2)$
$-2\mu = 4 \implies \mu = -2$

Substitute $\mu = -2$ in (ii):
$\lambda - (-2) = -2 \implies \lambda = -4$

Substitute $\lambda = -4$ into Line 1 equation to find the point:
$x = 3 + (-4) = -1$
$y = 2 + 2(-4) = -6$
$z = -4 + 2(-4) = -12$

Final Answer: $\boxed{ \text{Shortest Distance = }0. \text{ Point of Intersection = } (-1, -6, -12) }$ .

Q33 (Alternative): Find the vector equation of the line passing through $(1,2,-4)$ and perpendicular to the two lines: $\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}$ and $\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}$ .

Solution:
Step 1: Identify Direction Vectors.
Line 1 Direction ( $\vec{b_1}$ ): $3\hat{i} - 16\hat{j} + 7\hat{k}$
Line 2 Direction ( $\vec{b_2}$ ): $3\hat{i} + 8\hat{j} - 5\hat{k}$

Step 2: Find Direction of Required Line.
Since the required line is perpendicular to both, its direction $\vec{b}$ is the cross product $\vec{b_1} \times \vec{b_2}$ .

$\vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}$

$\vec{b} = \hat{i}(80 - 56) - \hat{j}(-15 - 21) + \hat{k}(24 - (-48))$
$\vec{b} = 24\hat{i} + 36\hat{j} + 72\hat{k}$

Simplify the direction ratios by dividing by 12:
$\vec{b} = 2\hat{i} + 3\hat{j} + 6\hat{k}$

Step 3: Writing the Vector Equation of the required line
Passes through point $\vec{a} = \hat{i} + 2\hat{j} - 4\hat{k}$ .
Formula: $\vec{r} = \vec{a} + \lambda\vec{b}$
$\vec{r} = (\hat{i} + 2\hat{j} - 4\hat{k}) + \lambda(2\hat{i} + 3\hat{j} + 6\hat{k})$

Final Answer: $\boxed{ \vec{r} = (\hat{i} + 2\hat{j} - 4\hat{k}) + \lambda(2\hat{i} + 3\hat{j} + 6\hat{k}) }$

Q34: Using integration, find the area of $\triangle ABC$ , whose vertices are $A(2,0)$ , $B(4,5)$ and $C(6,3)$ .

Solution:
Step 1: Find Equations of Lines.
Equation of AB: Points (2,0) and (4,5).
$y - 0 =\frac{5-0}{4-2}(x-2) \implies y = \frac{5}{2}(x-2)$

Equation of BC: Points (4,5) and (6,3).
$y - 5 =\frac{3-5}{6-4}(x-4) \implies y - 5 = -1(x-4) \implies y = 9-x$

Equation of AC: Points (2,0) and (6,3).
$y - 0 =\frac{3-0}{6-2}(x-2) \implies y = \frac{3}{4}(x-2)$

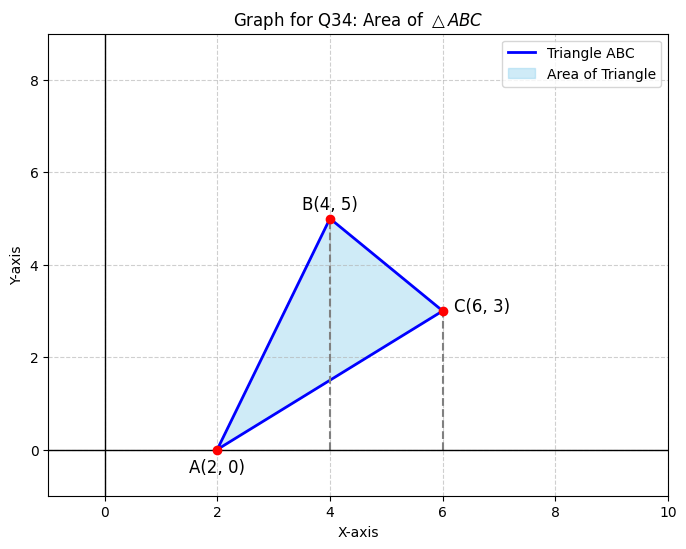
Step 2: Set up the Definite Integral.
Area = Area under AB + Area under BC – Area under AC.

Area = $\int_{2}^{4} y_{AB} dx + \int_{4}^{6} y_{BC} dx - \int_{2}^{6} y_{AC} dx$

Step 3: Evaluate Integrals.
$\int_{2}^{4} \frac{5}{2}(x-2) dx = \frac{5}{2} [\frac{x^2}{2} - 2x]_2^4$

$= \frac{5}{2} [(8-8) - (2-4)] = \frac{5}{2}[2] = 5$

$\int_{4}^{6} (9-x) dx = [9x - \frac{x^2}{2}]_4^6$

$= (54 - 18) - (36 - 8) = 36 - 28 = 8$

$\int_{2}^{6} \frac{3}{4}(x-2) dx = \frac{3}{4} [\frac{x^2}{2} - 2x]_2^6$

$= \frac{3}{4} [(18 - 12) - (2 - 4)] = \frac{3}{4} [6 - (-2)] = \frac{3}{4}(8) = 6$

Step 4: Calculate Total Area.
$Area = 5 + 8 - 7= 7$

Final Answer: $\boxed{ 7 \text{ sq units.} }$

Q35: If $A=\begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix}$ , find $A^{-1}$ and hence solve the system of linear equations: $2x-3y+5z=11$ , $3x+2y-4z=-5$ , $x+y-2z=-3$ .

Solution:
Step 1: Calculate Determinant |A|.
$|A| = 2(-4 + 4) - (-3)(-6+4) + 5(3-2)$

$|A| = 2(0) + 3(-2) + 5(1)$

$|A| = 0 - 6 + 5 = -1$
Since $|A| \ne 0$ , $A^{-1}$ exists.

Step 2: Find Cofactors.

$A_{11} = 0, A_{12} = 2, A_{13} = 1$

$A_{21} = -(6-5)=-1, A_{22} = -4-5=-9, A_{23} = -(2+3)=-5$

$A_{31} = 12-10=2, A_{32} = -(-8-15)=-23, A_{33} = 4+9=13$

Step 3: Finding Adjoint and Inverse.
$adj A = \begin{bmatrix} 0 & -1 & 2 \\ 2 & -9 & 23 \\ 1 & -5 & 13 \end{bmatrix}$ (Transpose of Cofactor Matrix)

$A^{-1} = \frac{1}{|A|} adj A = \frac{1}{-1} \begin{bmatrix} 0 & -1 & 2 \ 2 & -9 & 23 \ 1 & -5 & 13 \end{bmatrix}$

$A^{-1} = \begin{bmatrix} 0 & 1 & -2 \ -2 & 9 & -23 \ -1 & 5 & -13 \end{bmatrix}$

Step 4: Solve the System of Equations.
The system can be written as $AX = B$ ,
where $X = \begin{bmatrix} x \ y \ z \end{bmatrix}$ and
$B = \begin{bmatrix} 11 \ -5 \ -3 \end{bmatrix}$ .

Solution is $X = A^{-1}B$ .

$\begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 & 1 & -2 \\ -2 & 9 & -23 \\ -1 & 5 & -13 \end{bmatrix} \begin{bmatrix} 11 \\ -5 \\ -3 \end{bmatrix}$

Multiply the matrices:
$x = 0(11) + 1(-5) + (-2)(-3) = 0 - 5 + 6 = 1$
$y = -2(11) + 9(-5) + (-23)(-3) = -22 - 45 + 69 = -67 + 69 = 2$
$z = -1(11) + 5(-5) + (-13)(-3) = -11 -25 + 39 = -36 + 39 = 3$

Final Answer: $x = 1, y = 2, z = 3$

Section E: Case Study Based Questions, 4 Marks (1+1+2)

Q36: Case-Study 1 Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation $\frac{dy}{dx} = k(50-y) where x denotes the number of weeks and y the number of children who have been given the drops. (i) State the degree of the above given differential Equation (ii) How arbitrary constants do the general solution of the above differential equation has? (iii) Given that y(0) = 0 and k = 0.049 find the particular solution of the differential equation. OR (iii) Find the equation which gives the number of children who have been given polio drop up till week x. </p><p><strong>Solution:</strong> [latex] x$ denotes the number of weeks.
$y$ denotes the number of children (in thousands) who have been given the drops.
Total population is 50 (representing 50,000).

(i) State the degree of the above given differential Equation.
Step 1: Identify the order and degree. The given differential equation is $\frac{dy}{dx} = k(50-y)$ .
Order: The highest order derivative is $\frac{dy}{dx}$ (First Order).
Degree: The power of the highest order derivative is 1.

Final Answer: The degree of the differential equation is 1.

(ii) How many arbitrary constants does the general solution of the above differential equation have?
Step 1: Relate order to constants.
The number of arbitrary constants in the general solution of a differential equation is equal to the order of the differential equation. Since this is a first-order differential equation, it has 1 arbitrary constant.

Final Answer: 1

(iii) Given that $y(0)=0$ and $k=0.049$ , find the particular solution of the differential equation.
Step 1: Separate variables and integrate.
$\frac{dy}{50-y} = k dx$

Integrating both sides:
$\int \frac{1}{50-y} \ dy = \int k dx$

$-\ln|50-y| = kx + C$

Step 2: Simplify the equation.
$\ln|50 - y| = -kx - C$

$50-y = e^{-kx-C}$

$50-y = e^{-C} \cdot e^{-kx}$

Let $A = e^{-C}$ .

$50-y = A e^{-kx}$

$y = 50 - A e^{-kx}$

Step 3: Apply initial condition $y(0) = 0$ .
When $x = 0$ , $y = 0$ .

$0 = 50 - A e^{0}$
$0 = 50 - A \implies A = 50$
So, the general form is: $y = 50(1 - e^{-kx})$ .

Step 4: Substitute $k = 0.049$ .
$y = 50(1 - e^{-0.049x})$ .

Final Answer: $\boxed{ y = 50(1 - e^{-0.049x}) }$

(iii) Find the equation which gives the number of children who have been given polio drop up till week x.
Step 1: Use the data from the problem statement.
We know $y(0) = 0$ and at the end of the 2nd week ( $x=2$ ), half the children ( $y=25$ ) have been given drops.

Step 2: Use the solution form from (iii).
$y = 50(1 - e^{-kx})$

Substitute $x=2, y=25$ :

$25 = 50(1 - e^{-2x})$

$\frac{25}{50} = 1 - e^{-2k}$

$\frac{1}{2} = 1 - e^{-2k}$

$e^{-2k} = 0.5$ Taking log on both sides:

$-2k = \ln(0.5)$
$-2k = -\ln(2)$
$k = \frac{1}{2} \ln 2$

Step 3: Write the final equation.
$y = 50(1 - e^{-\frac{x}{2} \ln 2})$

Or simply substituting the value of $e^{-k}$ :

Since $e^{-2k} = 1/2 \implies e^{-k} = (1/2)^{1/2} = \frac{1}{\sqrt{2}}$ .

$y = 50(1 - (\frac{1}{\sqrt{2}})^x)$

Final Answer: $\boxed { y = 50(1 - e^{-\frac{x}{2} \ln 2}) }$

Q37: Case-Study 2: A gardener wants to construct a rectangular bed of garden in a circular patch of land. He takes the maximum perimeter of the rectangular region as possible. (Refer to the images given below for calculations)

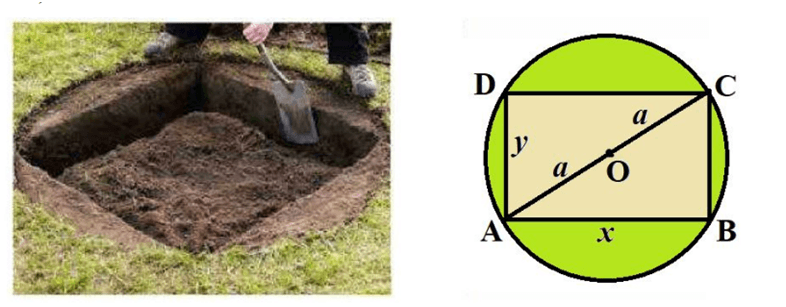
(i) Find the perimeter of rectangle in terms of any one side and radius of circle.
(ii) Find critical points to maximize the perimeter of rectangle?
(iii) Check for maximum or minimum value of perimeter at critical point.
OR
(iii) If a rectangle of the maximum perimeter which can be inscribed in a circle of radius 10 cm is square, then the perimeter of region

Solution:
(i) Find the perimeter of rectangle in terms of any one side and radius of circle.
Step 1: Define variables.
Let the radius of the circle be $a$ .
Let the length of the rectangle be $x$ and the breadth be $y$ .
The diagonal of the inscribed rectangle passes through the center and is equal to the diameter ( $2a$ ).

Step 2: Establish the relationship between x, y, and a.
Using Pythagoras theorem in the right triangle formed by sides $x, y$ and diagonal $2a$ :
$x^2 + y^2 = (2a)^2$

$y^2 = 4a^2 - x^2$

$y = \sqrt{4a^2 - x^2}$

Step 3: Formulate Perimeter (P).
Perimeter $P = 2(x + y)$ Substitute $y$ :
$P(x) = 2(x + \sqrt{4a^2 - x^2})$

Final Answer: $\boxed{ P = 2(x + \sqrt{4a^2 - x^2}) }$

(ii) Find critical points to maximize the perimeter of rectangle?
Step 1: Differentiate P with respect to x.

$P'(x) = \frac{d}{dx} [ 2(x + \sqrt{4a^2 - x^2})]$ ]

$P'(x) = 2 \left( 1 + \frac{1}{2\sqrt{4a^2 - x^2}} \cdot (-2x) \right)$

$P'(x) = 2 \left( 1 - \frac{x}{\sqrt{4a^2 - x^2}} \right)$

Step 2: Set $P'(x) = 0$ to find critical points.
$1 - \frac{x}{\sqrt{4a^2 - x^2}} = 0$

$1 = \frac{x}{\sqrt{4a^2 - x^2}}$

$\sqrt{4a^2 - x^2} = x$

Step 3: Solve for x. Squaring both sides:
$4a^2 - x^2 = x^2$
$2x^2 = 4a^2$
$x^2 = 2a^2$
$x = \sqrt{2}a$

Final Answer: The critical point is $\boxed{ x = \sqrt{2}a }$ .

(iii) Check for maximum or minimum value of perimeter at critical point.

Step 1: Use the First Derivative Test.
For $x < \sqrt{2}a$ , $\sqrt{4a^2 - x^2} > x$ , so $\frac{x}{\sqrt{4a^2-x^2}} < 1$ . Thus $P'(x) > 0$ .
For $x > \sqrt{2}a$ , $\sqrt{4a^2 - x^2} < x$ , so $\frac{x}{\sqrt{4a^2-x^2}} > 1$ . Thus $P'(x) < 0$ .

Since the derivative changes from positive to negative, $x = \sqrt{2}a$ is a point of Maxima.

Answer: The perimeter is Maximum at the critical point.

(iii) If a rectangle of the maximum perimeter which can be inscribed in a circle of radius 10 cm is square, then the perimeter of region.
Step 1: Identify dimensions.
From part (ii), max perimeter occurs at $x = \sqrt{2}a$ . Corresponding $y = \sqrt{4a^2 - 2a^2} = \sqrt{2}a$ .
Since $x = y$ , the rectangle is indeed a square.
Given radius $a = 10$ cm.

Step 2: Calculate side length.
Side $x = 10\sqrt{2}$ cm.

Step 3: Calculate Perimeter.
Perimeter $= 4x$
$= 4(10\sqrt{2})$
$= 40\sqrt{2}$ cm.

Final Answer: $\boxed{ Perimeter = 40\sqrt{2}}$ cm.

Q38: Case-Study 3: In a test, you either guess or copies or knows the answer to a multiple-choice question with four choice. The probability that you make a guess is 1/3, you copy the answer is 1/6. The probability that your answer is correct, given that you guess it, is 1/8. And also, the probability that you answer is correct, given that you copy it, is 1/4.

Solution:
Given
Probability of guessing $P(G) = 1/3$
Probability of copying $P(C) = 1/6$
Probability of knowing $P(K)$ is the remaining probability.
Probability Answer is Correct given Guess $P(R|G) = 1/8$
Probability Answer is Correct given Copy $P(R|C) = 1/4$
Probability Answer is Correct given Know $P(R|K) = 1$ (Implied, as knowing the answer means answering correctly).

(i) The probability that you know the answer.
The events Guess, Copy, and Know are mutually exclusive and exhaustive.
$P(G) + P(C) + P(K) = 1$

$1/3 + 1/6 + P(K) = 1$

$3/6 + P(K) = 1 \implies P(K) = 1 - 1/2 = 1/2$

Final Answer: $\boxed{ P(K) = 1/2}$

(ii) Find the probability that your answer is correct given that you guess it and the probability that your answer is correct given that you know the answer.
Probability correct given guess:

Final Answer: $\boxed{ P(R|G) = 1/8}$

Probability correct given know:
If a student knows the answer, they will mark it correctly.

Final Answer: $\boxed{ P(R|K) = 1}$

(iii) Find the probability that you know the answer given that you correctly answered it.
We need to find $P(K|R)$ . Using Bayes' Theorem:
$P(K|R) = \frac{P(R|K) P(K)}{P(R)}$

First, calculate total probability of being correct $P(R)$ :
$P(R) = P(R|G)P(G) + P(R|C)P(C) + P(R|K)P(K)$

$P(R) = (1/8 \times 1/3) + (1/4 \times 1/6) + (1 \times 1/2)$

$P(R) = 2/24 + 12/24 = 14/24 = 7/12$

Now, apply Bayes' Theorem:
$P(K|R) = \frac{1 \times 1/2} {7/12}$

$P(K|R) = \frac{1/2}{7/12} = \frac{1}{2} \times \frac{12}{7} = \frac{6}{7}$

Final Answer: $\boxed{ P(K|R) = \frac{6}{7}}$

(iii) Find the total probability of correctly answered the question.
This was calculated in the previous step as the denominator.
$P(R) = P(R|G)P(G) + P(R|C)P(C) + P(R|K)P(K)$

$P(R) = 1/24 + 1/24 + 1/2$

$P(R) = 7/12$

Final Answer: $P(R) = 7/12$

Section A: 1 mark questions

Q1: Find the cofactor of a_{12} in the following: \begin{vmatrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{vmatrix}

Q2: If \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 3 & 1 \\ 2 & 5 \end{bmatrix} = \begin{bmatrix} 7 & 11 \\ k & 23 \end{bmatrix} , then write the value of k.

Q3: If y = \sqrt{a^{2}-x^{2}} , then y\frac{dy}{dx} is:

Q4: If f(x)=x^{2}sin\frac{1}{x} where x\ne0 , then the value of the function f at x=0 so that the function is continuous at x=0 is:

Q5: The value of \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{dx}{1+\sqrt{\tan x}} is:

Q6: If m and n are the order and degree, respectively of the differential equation y{(\frac{dy}{dx})}^{3}+x^{3}(\frac{d^{2}y}{dx^{2}})^{2}-xy=sin~x, then write the value of m+n .

Q7: The magnitude of each of the two vectors \vec{a} and \vec{b} , having the same magnitude such that the angle between them is 60^{\circ} and their scalar product is 9/2 is:

Q8: Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F=4x+6y be the objective function. The minimum value of F occurs at:

Q9: If a line makes angles \alpha, \beta, \gamma with the positive direction of co-ordinates axes, then find the value of sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma .

Q10: The projection of the vector 2\hat{i}+3\hat{j}+2\hat{k} on the vector \hat{i}+2\hat{j}+\hat{k} is

Q12: The value of \int_{1}^{2}\frac{dx}{x\sqrt{x^{2}-1}} is

Q13: If x\begin{bmatrix} 2 \\ 3 \end{bmatrix} + y\begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix} , find the value of x.

Q14: Feasible region (shaded) for a LPP is shown in the given figure. The maximum value of the Z=0.4x+y is

Q15: If \begin{vmatrix} 2x+5 & 3 \\ 5x+2 & 9 \end{vmatrix} = 0 , find x.

Q16: If A is a non-singular matrix of order 3 and |A|=-4 , find |adj A| .

Q17: The straight line \frac{x-3}{3}=\frac{y-2}{1}=\frac{z-1}{0} is:

Q18: If |\vec{a}|=10 , |\vec{b}|=2 and \vec{a} \cdot \vec{b}=12 , then the value of |\vec{a} \times \vec{b}| is

Q19: Assertion (A): The angle between the straight lines \frac{x-1}{1}=\frac{y+2}{2}=\frac{z-3}{-3} and \frac{x+1}{2}=\frac{y-2}{5}=\frac{z+3}{4} is 90^{\circ} . Reason (R): Skew lines are lines in different planes which are parallel and intersecting.

Q20: Assertion (A): Domain of f(x)=sin^{-1}x+cos~x is [-1,1] . Reason (R): Domain of a function is the set of all possible values for which function will be defined.

Section B: 2 Marks Questions

Q21: If y=log(cos~e^{x}) , then find \frac{dy}{dx} .

Q22: (A) Prove that the Greatest Integer Function f:R\rightarrow R given by f(x)=[x] is neither one-one nor onto. Where [x] denotes the greatest integer less than or equal to x.

Q22: (B) If sin(sin^{-1}\frac{1}{5}+cos^{-1}x)=1, then find the value of x.

Q23: If |\vec{a}\times\vec{b}|^{2}+(\vec{a}.\vec{b})^{2}=144 and |\vec{a}|=4 , then find the value of |\vec{b}| .

Q24: (A) A pair of dice is thrown. Find the probability of getting 7 as the sum, if it is known that the second die always exhibits an odd number.

Q24: (B) A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event ‘number is even’ and B be the event ‘number is marked red’. Find whether the events A and B are independent or not.

Q25: If xy=log~y+C , then show that \frac{dy}{dx}=\frac{y^{2}}{1-xy} .

Section C: 3 Marks Questions

Q26: The scalar product of the vector \vec{a}=\hat{i}+\hat{j}+\hat{k} with a unit vector along the sum of the vectors \vec{b}=2\hat{i}+4\hat{j}-5\hat{k} and \vec{c}=\mu\hat{i}+2\hat{j}+3\hat{k} is equal to one. Find the value of \mu and hence find the unit vector along \vec{b}+\vec{c} .

Q26: Find the points on the line \frac{(x+2)}{3}=\frac{(y+1)}{2}=\frac{(z-3)}{2} at a distance of 3\sqrt{2} units from the point P(1,2,3) .

Q27: Evaluate: \int\frac{x^{2}+1}{(x^{2}+2)(x^{2}+3)}dx

Q28: (A) Evaluate: \int_{0}^{\pi}\frac{x~sin~x}{1+cos^{2}x}dx

Q28: (B) Evaluate: \int_{1}^{3}|x^{2}-2x|dx

Q29: Find the general solution of the following differential equation: (x^{2}-y^{2})dx+2xy~dy=0 .

Q29: (B) Solve: x \log x \frac{dy}{dx} + y = \frac{2}{x} \log x .

Q30: Solve the following Linear Programming Problem graphically: Minimize Z=13x-15y subject to the constraints x+y\le7, 2x-3y+6\ge0 , x\ge0 and y\ge0 .

Q31: Evaluate: \int e^{x}\frac{(1-sin~x)}{(1-cos~x)}dx .

Section D: 5 Marks Questions

Q32: Show that each of the relation R in the set A={x\in Z:0\le x\le12} , given by R={(a,b):|a-b| \text{ is a multiple of 4}} is an equivalence relation. Find the set of all elements related to 1 in each case.

Q32 (Alternative): Let A=R-{2} and B=R-{1} . If f:A\rightarrow B is a function defined by f(x)=\frac{x-1}{x-2} , then show that f is one-one and onto.

Q33: Find the shortest distance between the lines \vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+\lambda(\hat{i}+2\hat{j}+2\hat{k}) and \vec{r}=5\hat{i}-2\hat{j}+\mu(3\hat{i}+2\hat{j}+6\hat{k}) . If the lines intersect find their point of intersection.

Q33 (Alternative): Find the vector equation of the line passing through (1,2,-4) and perpendicular to the two lines: \frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7} and \frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5} .

Q34: Using integration, find the area of \triangle ABC , whose vertices are A(2,0) , B(4,5) and C(6,3) .

Q35: If A=\begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix} , find A^{-1} and hence solve the system of linear equations: 2x-3y+5z=11 , 3x+2y-4z=-5 , x+y-2z=-3 .

Section E: Case Study Based Questions, 4 Marks (1+1+2)

Leave a Comment Cancel Reply

Q1: Find the cofactor of $a_{12}$ in the following: $\begin{vmatrix} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{vmatrix}$

Q2: If $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 3 & 1 \\ 2 & 5 \end{bmatrix} = \begin{bmatrix} 7 & 11 \\ k & 23 \end{bmatrix}$ , then write the value of k.

Q3: If $y = \sqrt{a^{2}-x^{2}}$ , then $y\frac{dy}{dx}$ is:

Q4: If $f(x)=x^{2}sin\frac{1}{x}$ where $x\ne0$ , then the value of the function f at $x=0$ so that the function is continuous at $x=0$ is:

Q5: The value of $\int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\frac{dx}{1+\sqrt{\tan x}}$ is:

Q6: If m and n are the order and degree, respectively of the differential equation $y{(\frac{dy}{dx})}^{3}+x^{3}(\frac{d^{2}y}{dx^{2}})^{2}-xy=sin~x,$ then write the value of $m+n$ .

Q7: The magnitude of each of the two vectors $\vec{a}$ and $\vec{b}$ , having the same magnitude such that the angle between them is $60^{\circ}$ and their scalar product is $9/2$ is:

Q8: Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let $F=4x+6y$ be the objective function. The minimum value of F occurs at:

Q9: If a line makes angles $\alpha, \beta, \gamma$ with the positive direction of co-ordinates axes, then find the value of $sin^{2}\alpha+sin^{2}\beta+sin^{2}\gamma$ .

Q10: The projection of the vector $2\hat{i}+3\hat{j}+2\hat{k}$ on the vector $\hat{i}+2\hat{j}+\hat{k}$ is

Q12: The value of $\int_{1}^{2}\frac{dx}{x\sqrt{x^{2}-1}}$ is

Q13: If $x\begin{bmatrix} 2 \\ 3 \end{bmatrix} + y\begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} 10 \\ 5 \end{bmatrix}$ , find the value of x.

Q14: Feasible region (shaded) for a LPP is shown in the given figure. The maximum value of the $Z=0.4x+y$ is

Q15: If $\begin{vmatrix} 2x+5 & 3 \\ 5x+2 & 9 \end{vmatrix} = 0$ , find x.

Q16: If A is a non-singular matrix of order 3 and $|A|=-4$ , find $|adj A|$ .

Q17: The straight line $\frac{x-3}{3}=\frac{y-2}{1}=\frac{z-1}{0}$ is:

Q18: If $|\vec{a}|=10$ , $|\vec{b}|=2$ and $\vec{a} \cdot \vec{b}=12$ , then the value of $|\vec{a} \times \vec{b}|$ is

Q19: Assertion (A): The angle between the straight lines $\frac{x-1}{1}=\frac{y+2}{2}=\frac{z-3}{-3}$ and $\frac{x+1}{2}=\frac{y-2}{5}=\frac{z+3}{4}$ is $90^{\circ}$ .

Reason (R): Skew lines are lines in different planes which are parallel and intersecting.

Q20: Assertion (A): Domain of $f(x)=sin^{-1}x+cos~x$ is $[-1,1]$ .

Reason (R): Domain of a function is the set of all possible values for which function will be defined.

Q21: If $y=log(cos~e^{x})$ , then find $\frac{dy}{dx}$ .

Q22: (A) Prove that the Greatest Integer Function $f:R\rightarrow R$ given by $f(x)=[x]$ is neither one-one nor onto.
Where $[x]$ denotes the greatest integer less than or equal to x.

Q22: (B) If $sin(sin^{-1}\frac{1}{5}+cos^{-1}x)=1,$ then find the value of x.

Q23: If $|\vec{a}\times\vec{b}|^{2}+(\vec{a}.\vec{b})^{2}=144$ and $|\vec{a}|=4$ , then find the value of $|\vec{b}|$ .

Q25: If $xy=log~y+C$ , then show that $\frac{dy}{dx}=\frac{y^{2}}{1-xy}$ .

Q26: The scalar product of the vector $\vec{a}=\hat{i}+\hat{j}+\hat{k}$ with a unit vector along the sum of the vectors $\vec{b}=2\hat{i}+4\hat{j}-5\hat{k}$ and $\vec{c}=\mu\hat{i}+2\hat{j}+3\hat{k}$ is equal to one. Find the value of $\mu$ and hence find the unit vector along $\vec{b}+\vec{c}$ .

Q26: Find the points on the line $\frac{(x+2)}{3}=\frac{(y+1)}{2}=\frac{(z-3)}{2}$ at a distance of $3\sqrt{2}$ units from the point $P(1,2,3)$ .

Q27: Evaluate: $\int\frac{x^{2}+1}{(x^{2}+2)(x^{2}+3)}dx$

Q28: (A) Evaluate: $\int_{0}^{\pi}\frac{x~sin~x}{1+cos^{2}x}dx$

Q28: (B) Evaluate: $\int_{1}^{3}|x^{2}-2x|dx$

Q29: Find the general solution of the following differential equation: $(x^{2}-y^{2})dx+2xy~dy=0$ .

Q29: (B) Solve: $x \log x \frac{dy}{dx} + y = \frac{2}{x} \log x$ .

Q30: Solve the following Linear Programming Problem graphically: Minimize $Z=13x-15y$ subject to the constraints $x+y\le7,$ $2x-3y+6\ge0$ , $x\ge0$ and $y\ge0$ .

Q31: Evaluate: $\int e^{x}\frac{(1-sin~x)}{(1-cos~x)}dx$ .

Q32: Show that each of the relation R in the set $A={x\in Z:0\le x\le12}$ , given by $R={(a,b):|a-b| \text{ is a multiple of 4}}$ is an equivalence relation. Find the set of all elements related to 1 in each case.

Q32 (Alternative): Let $A=R-{2}$ and $B=R-{1}$ . If $f:A\rightarrow B$ is a function defined by $f(x)=\frac{x-1}{x-2}$ , then show that f is one-one and onto.

Q33: Find the shortest distance between the lines $\vec{r}=3\hat{i}+2\hat{j}-4\hat{k}+\lambda(\hat{i}+2\hat{j}+2\hat{k})$ and $\vec{r}=5\hat{i}-2\hat{j}+\mu(3\hat{i}+2\hat{j}+6\hat{k})$ . If the lines intersect find their point of intersection.

Q33 (Alternative): Find the vector equation of the line passing through $(1,2,-4)$ and perpendicular to the two lines: $\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}$ and $\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}$ .

Q34: Using integration, find the area of $\triangle ABC$ , whose vertices are $A(2,0)$ , $B(4,5)$ and $C(6,3)$ .

Q35: If $A=\begin{bmatrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{bmatrix}$ , find $A^{-1}$ and hence solve the system of linear equations: $2x-3y+5z=11$ , $3x+2y-4z=-5$ , $x+y-2z=-3$ .