Solution of: Class 12 Maths Relation and Function and Inverse Trigonometry Test 1 – 2026

Introduction

Have you solved Class 12 CBSE Relations & Functions and Inverse Trigonometry Test – 1 2026 and are looking for a solutions to the questions? Here you’ll find complete, step-by-step NCERT-style solutions for every question. Designed for both students and teachers, these answers make board exam revision easier with clear explanations, formula highlights, and downloadable PDF options.

Section A: 1 mark questions

Q1: A relation R is defined on N (the set of Natural Numbers). Which one of the following is a reflexive relation?

(A) R = {(x,y): x > y, \forall x, y \in N}
(B) R = {(x,y): x + y = 10, \forall x, y \in N}
(C) R = {(x,y): xy \text{ is a square number}, \forall x, y \in N}
(D) R = {(x,y): x + 4y = 10, \forall x, y \in N}

Solution:
Step 1: Understand the Condition for Reflexivity
For a relation R to be reflexive on a set N, the element must be related to itself.
Mathematically, (x, x) \in R for all x \in N.

Step 2: Check Option (A)
The condition given is x > y.
For reflexivity, we substitute y with x. Check: Is x > x?
No, a number is never strictly greater than itself.
Result: Not Reflexive.

Step 3: Check Option (B)
The condition given is x + y = 10.
Substitute y with x.
Check: x + x = 10 \Rightarrow 2x = 10 \Rightarrow x = 5.
This relation holds true only if x = 5.
It does not hold for other natural numbers (e.g., 1 + 1 \neq 10).
Result: Not Reflexive.

Step 4: Check Option (C)
The condition given is that xy is a square number.
Substitute y with x. Check: x \cdot x = x^2.
Since x is a natural number, x^2 is always a perfect square.
This holds true for every x \in N.
Result: Reflexive.

Step 5: Check Option (D)
The condition given is x + 4y = 10.
Substitute y with x.
Check: x + 4(x) = 10 \Rightarrow 5x = 10 \Rightarrow x = 2.
This relation holds true only if x = 2.
It does not hold for all natural numbers.
Result: Not Reflexive.

Correct Option: (C)

Q2: Let f:R\rightarrow R be defined by f(x)=\frac{1}{x} for all x\in R, then f is

(A) onto
(B) one-one
(C) bijective
(D) Not Defined

Solution:
Step 1: Analyze the Domain
The function is defined as f(x) = \frac{1}{x} for all x \in R (the set of Real Numbers).
The set R includes the number 0.

Step 2: Check for Validity at x = 0
If we substitute x = 0 into the function, we get f(0) = \frac{1}{0}.
Division by zero is undefined in mathematics.

Step 3: Conclusion
Since the image of 0 \in R does not exist, f is not a valid function on the given domain R. Therefore, the function is not defined.

Correct Option: (D)

Q3: sin[cot^{-1}{tan(cos^{-1}x)}] is equal to

(A) x
(B) \sqrt{1-x^{2}}
(C) \frac{1}{x}
(D) None of these

Solution:
Step 1: Simplify the Inner Term
Let cos^{-1}x = \theta.
Then cos \theta = x.
From a right-angled triangle where the adjacent side is x and the hypotenuse is 1,
the opposite side is \sqrt{1-x^2}.
Therefore, tan \theta = \frac{\sqrt{1-x^2}}{x}.

The expression becomes: sin[cot^{-1}(tan \theta)] = sin[cot^{-1}(\frac{\sqrt{1-x^2}}{x})].

Step 2: Simplify the Next Term
Let cot^{-1}(\frac{\sqrt{1-x^2}}{x}) = \phi.

This implies cot \phi = \frac{\sqrt{1-x^2}}{x}.

In a right-angled triangle for angle \phi:
Base (Adjacent) = \sqrt{1-x^2}

Perpendicular (Opposite) = x

Hypotenuse = \sqrt{(\sqrt{1-x^2})^2 + x^2} = \sqrt{1-x^2 + x^2} = \sqrt{1} = 1.

Step 3: Evaluate the Final Sine Function
We need to find sin \phi.
sin \phi = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{x}{1} = x.

Correct Option: (A)

Q4: The number of relations that can be defined on the set A={3,5,7} are

(A) 9
(B) 512
(C) 256
(D) 2^{6}

Solution:
Step 1: Determine the Number of Elements
The set A has 3 elements: {3, 5, 7}.
So, n(A) = 3.

Step 2: Calculate Total Elements in Cartesian Product
The Cartesian product A \times A has n(A) \times n(A) elements. 3 \times 3 = 9 elements.

Step 3: Calculate Number of Relations
A relation is a subset of A \times A.
The total number of subsets (relations) is given by 2^{n(A \times A)}.
Number of relations = 2^9.

Step 4: Simplify Value 2^9 = 512.

Correct Option: (B)

Q5: Let the relation R in the set A={x\in Z:0\le x\le12}, given by R={(a,b):|a-b| is a multiple of 4}. Then [1], the equivalence class containing 1 is

(A) {1,5,9}
(B) {3, 7, 11}
(C) A
(D) {0, 1, 2, 5}

Solution:
Step 1: Understand Equivalence Class [1]
The equivalence class [1] consists of all x \in A such that (x, 1) \in R.
This means |x - 1| must be a multiple of 4.
Mathematically, x - 1 = 4k or x = 4k + 1 for some integer k.

Step 2: Find Elements in A
The set A = {0, 1, 2, ..., 12}.
We test values of k to find x within the range [0, 12]:
If k = 0 \Rightarrow x = 1
If k = 1 \Rightarrow x = 1 + 4 = 5
If k = 2 \Rightarrow x = 1 + 8 = 9
If k = 3 \Rightarrow x = 1 + 12 = 13 (Outside set A)

Step 3: List the Set The elements are {1, 5, 9}.

Correct Option: (A)

Q6: If tan^{-1}(cot~A)=2A, then A=

(A) \pm\frac{\pi}{3}

(B) \pm\frac{\pi}{4}

(C) \pm\frac{\pi}{6}

(D) None of these

Solution:
Step 1: Convert Cot to Tan
We know that \cot A = \tan(\frac{\pi}{2} - A).
Substituting this into the LHS:
\tan^{-1}(\tan(\frac{\pi}{2} - A) = 2A

Step 2: Eliminate Inverse Function Assuming the value lies within the principal branch:
\frac{\pi}{2} - A = 2A

Step 3: Solve for A
\frac{\pi}{2} = 3A

A = \frac{\pi}{6}

Correct Option: (C)

Q7: Let A={1,2,3}, B={4,5,6,7} and let f={(1,4), (2,5), (3,6)} be a function from A to B. Based on the above information f is best defined as

(A) Surjective Function
(B) Injective Function
(C) Bijective Function
(D) None of these

Solution:
Step 1: Check for Injectivity (One-One)
A function is injective if distinct elements of the domain have distinct images.
f(1) = 4
f(2) = 5
f(3) = 6

All images (4, 5, 6) are unique.
Therefore, f is Injective.

Step 2: Check for Surjectivity (Onto)
A function is surjective if every element in the co-domain B is the image of some element in A.
Co-domain B = {4, 5, 6, 7}.
Range of f = {4, 5, 6}.

The element 7 \in B has no pre-image in A.
Therefore, f is Not Surjective.

Step 3: Conclusion
Since it is one-one but not onto, it is an Injective function.

Correct Option: (B)

Section B: 2 marks questions

Q8: For the principal value evaluate sin^{-1}(-\frac{\sqrt{3}}{2})+cos^{-1}(\frac{\sqrt{3}}{2})

Solution:
Step 1: Evaluate the First Term
We need to find the principal value of sin^{-1}(-\frac{\sqrt{3}}{2}).

We know that the principal value branch of sin^{-1}x is [-\frac{\pi}{2}, \frac{\pi}{2}].

Using the property sin^{-1}(-x) = -sin^{-1}x: sin^{-1}(-\frac{\sqrt{3}}{2}) = -sin^{-1}(\frac{\sqrt{3}}{2}).

Since sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2},

we get: -sin^{-1}(\frac{\sqrt{3}}{2}) = -\frac{\pi}{3}.

Step 2: Evaluate the Second Term
We need to find the principal value of cos^{-1}(\frac{\sqrt{3}}{2}).

We know that the principal value branch of cos^{-1}x is [0, \pi].

Since cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2}, we get: cos^{-1}(\frac{\sqrt{3}}{2}) = \frac{\pi}{6}.

Step 3: Calculate the Final Sum
Substitute the values back into the original expression:
sin^{-1}(-\frac{\sqrt{3}}{2})+cos^{-1}(\frac{\sqrt{3}}{2}) = -\frac{\pi}{3} + \frac{\pi}{6}

sin^{-1}(-\frac{\sqrt{3}}{2})+cos^{-1}(\frac{\sqrt{3}}{2}) = \frac{-2\pi + \pi}{6} = -\frac{\pi}{6}.

Final Answer: \boxed{ sin^{-1}(-\frac{\sqrt{3}}{2})+cos^{-1}(\frac{\sqrt{3}}{2}) = -\frac{\pi}{6} }

Q9: Find the domain of \cos^{-1}(x^{2}-4)

Solution:
Step 1: Understand the Domain Condition
The domain of the inverse cosine function, \cos^{-1}(y), is defined for values in the interval [-1, 1].

Therefore, for cos^{-1}(x^{2}-4) to be defined, the argument (x^2 - 4) must satisfy the condition:

-1 \le x^2 -4 \le 1

Step 2: Solve the Inequality
-1+4 \le x^2 \le 1+4
3 \le x^2 \le 5

This can be broken down into two parts:
1. x^2 \ge 3 \Rightarrow x \in (-\infty, -\sqrt{3}] \cup [\sqrt{3}, \infty)

2. x^2 \le 5 \Rightarrow x \in [-\sqrt{5}, \sqrt{5}]

Step 3: Find the Intersection
We need values of x that satisfy both conditions simultaneously.
The intersection of the two sets is:
x \in [-\sqrt{5}, -\sqrt{3}] \cup [\sqrt{3}, \sqrt{5}]

Final Answer: \text{Domain} = [-\sqrt{5}, -\sqrt{3}] \cup [\sqrt{3}, \sqrt{5}]

Q10: Evaluate \sin^{-1}(\sin\frac{3\pi}{4})+\cos^{-1}(\cos\frac{3\pi}{4})+\tan^{-1}1

Solution:
Step 1: Evaluate the First Term
We need to evaluate \sin^{-1}(\sin\frac{3\pi}{4}).

The principal value branch of \sin^{-1}x is [-\frac{\pi}{2}, \frac{\pi}{2}].

The angle \frac{3\pi}{4} is outside this range.

We use the property \sin(\theta) = \sin(\pi - \theta):

\sin^{-1}(\sin\frac{3\pi}{4}) = \sin(\pi - \frac{\pi}{4}) = \sin(\frac{\pi}{4})

Therefore: \sin^{-1}(\sin\frac{3\pi}{4}) = \sin^{-1}(\sin\frac{\pi}{4}) = \frac{\pi}{4}.

Step 2: Evaluate the Second Term
We need to evaluate \cos^{-1}(\cos\frac{3\pi}{4}).

The principal value branch of \cos^{-1}x is [0, \pi].

Since \frac{3\pi}{4} lies within the range [0, \pi], the value is taken directly:

\cos^{-1}(\cos\frac{3\pi}{4}) = \frac{3\pi}{4}.

Step 3: Evaluate the Third Term
We need to evaluate \tan^{-1}(1).

We know that \tan(\frac{\pi}{4}) = 1.

Therefore: \tan^{-1}(1) = \frac{\pi}{4}.

Step 4: Calculate the Final Sum
Substitute the values back into the expression:
\sin^{-1}(\sin\frac{3\pi}{4})+\cos^{-1}(\cos\frac{3\pi}{4})+\tan^{-1}1 = \frac{\pi}{4} + \frac{3\pi}{4} + \frac{\pi}{4}

\sin^{-1}(\sin\frac{3\pi}{4})+\cos^{-1}(\cos\frac{3\pi}{4})+\tan^{-1}1 = \frac{\pi + 3\pi + \pi}{4} = \frac{5\pi}{4}

Final Answer: \boxed{ \sin^{-1}(\sin\frac{3\pi}{4})+\cos^{-1}(\cos\frac{3\pi}{4})+tan^{-1}1 = \frac{5\pi}{4}}

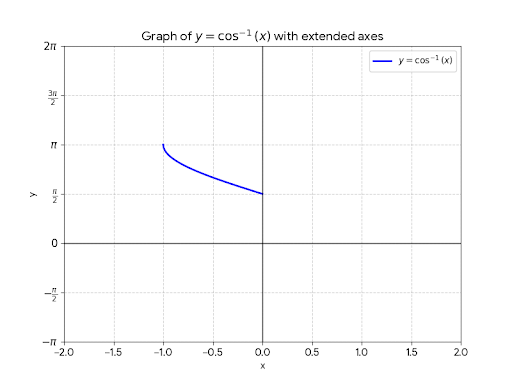
Q11: Draw the graph of \cos^{-1}x, where x\in[-1,0]. Also, write its range.

Solution:
Step 1: Analyze the Domain and Function
The function is given by f(x) = \cos^{-1} x. The restricted domain is given as x \in [-1, 0].

Step 2: Determine the Range
We know that the standard principal value branch of \cos^{-1} x is [0, \pi].
Let’s check the values at the endpoints of the given domain:

At x = -1:
\cos^{-1}(-1) = \pi

At x = 0:
\cos^{-1}(0) = \frac{\pi}{2}

Since the function \cos^{-1} x is a decreasing function, the values will lie between \frac{\pi}{2} and \pi.
Range: [\frac{\pi}{2}, \pi].

Step 3: Coordinates for the Graph
To draw the graph, we can plot specific points within the interval [-1, 0]:

• If x = -1, y = \pi
• If x = -\frac{\sqrt{3}}{2} , y = \frac{5\pi}{6}
• If x = -\frac{1}{2} = -0.5, y = \frac{2\pi}{3}
• If x = 0, y = \frac{\pi}{2}

Step 4: The Graph
The graph is a smooth curve starting from the point (-1, \pi) and decreasing down to (0, \frac{\pi}{2}).

Section C: 3 marks questions

Q12: Let S be the set of all points in a plane and R be a relation on S defined as R={(P,Q): \text{Distance between P and Q is less than 2 units}}. Show that R is reflexive and symmetric but not transitive.

Solution:
Step 1: Check for Reflexivity
For R to be reflexive, every point P \in S must be related to itself, i.e., (P, P) \in R.
The distance between a point P and itself is always 0.
Since 0 < 2, the condition is satisfied.
Therefore, (P, P) \in R.
Result: R is Reflexive.

Step 2: Check for Symmetry
Let P, Q \in S such that (P, Q) \in R.
This implies that the distance between P and Q is less than 2 units.
Since distance is independent of direction, Distance(P, Q) = Distance(Q, P).
Therefore, the distance between Q and P is also less than 2 units.
This implies (Q, P) \in R.
Result: R is Symmetric.

Step 3: Check for Transitivity
Let P, Q, S \in S such that (P, Q) \in R and (Q, S) \in R.
We need to check if (P, S) \in R.

• Let P, Q, S be three collinear points in that order.
• Let Distance(P, Q) = 1.5 units. Since 1.5 < 2, (P, Q) \in R.
• Let Distance(Q, S) = 1.5 units. Since 1.5 < 2, (Q, S) \in R.
• The total distance between P and S is 1.5 + 1.5 = 3 units.
• Since 3 > 2, the condition fails, and (P, S) \notin R.

Result: R is Not Transitive.
Conclusion: The relation is Reflexive and Symmetric but not Transitive.

Q13: Evaluate \tan(\cos^{-1}\frac{3}{5}+\tan^{-1}\frac{1}{4})

Solution:
Step 1: Convert Inverse Cosine to Inverse Tangent
We need to express \cos^{-1}\frac{3}{5} in terms of \tan^{-1}.

Let \cos^{-1}\frac{3}{5} = \theta.

Then \cos \theta = \frac{3}{5}.

In a right-angled triangle, if the Base is 3 and the Hypotenuse is 5, the Perpendicular is: P = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4.

Therefore, \tan \theta = \frac{Perpendicular}{Base} = \frac{4}{3}.

So, \cos^{-1}\frac{3}{5} = \tan^{-1}\frac{4}{3}.

Step 2: Substitute into the Expression
The expression becomes:
\tan(\tan^{-1}\frac{4}{3} + \tan^{-1}\frac{1}{4})

Step 3: Apply the Sum Formula
Use the identity \tan^{-1}x + \tan^{-1}y = \tan^{-1}(\frac{x+y}{1-xy}), provided xy < 1.

Here, x = \frac{4}{3} and y = \frac{1}{4}.

Check product: \frac{4}{3} \times \frac{1}{4} = \frac{1}{3} < 1. Condition satisfied.

Calculate the sum inside the bracket:
\tan^{-1} \left( \frac{\frac{4}{3} + \frac{1}{4}}{1 - (\frac{4}{3} \times \frac{1}{4})} \right)

Numerator: \frac{16 + 3}{12} = \frac{19}{12}

Denominator: 1 - \frac{1}{3} = \frac{2}{3}

Expression: \tan^{-1}\left( \frac{\frac{19}{12}}{\frac{2}{3}} \right) = \tan^{-1}\left( \frac{19}{12} \times \frac{3}{2} \right) = \tan^{-1}\left( \frac{19}{8} \right)

Step 4: Final Evaluation
Now we have \tan(\tan^{-1}\frac{19}{8}).

Using the property \tan(\tan^{-1}x) = x:

\tan(\tan^{-1}\frac{19}{8}) = \frac{19}{8}.

Final Answer: \boxed{\tan(\cos^{-1}\frac{3}{5}+\tan^{-1}\frac{1}{4}) = \frac{19}{8}}

Q14: Check if the following function f is bijective: f: Q-{3}\rightarrow Q defined by f(x)=\frac{2x+3}{x-3}

Solution:
Step 1: Check for Injectivity (One-One)
A function is injective if f(x_1) = f(x_2) \implies x_1 = x_2.

Let x_1, x_2 \in Q-{3} such that f(x_1) = f(x_2).
\frac{2x_1+3}{x_1-3} = \frac{2x_2+3}{x_2-3}

(2x_1+3)(x_2-3) = (2x_2+3)(x_1-3)

2x_1x_2 - 6x_1 + 3x_2 - 9 = 2x_1x_2 - 6x_2 + 3x_1 -9

- 6x_1 + 3x_2 = - 6x_2 + 3x_1

6x_2 + 3x_2 = 6x_1 + 3x_1

9x_2 = 9x_1

x_1 = x_2

Result: The function is Injective (One-One).

Step 2: Check for Surjectivity (Onto)
A function is surjective if for every y in the co-domain Q, there exists an x in the domain Q-{3} such that f(x) = y.
Let y = \frac{2x+3}{x-3}. Solve for x in terms of y:
y(x-3) - 2x+3

xy - 3y = 2x + 3

xy - 2x = 3y + 3

x(y-2) = 3y + 3

x = \frac{3y + 3}{y-2}

Step 3: Analyze the Range vs Co-domain
For x to be a rational number, the denominator y-2 must not be zero.
Therefore, y \neq 2.
This means the value 2 (which belongs to the co-domain Q) has no pre-image in the domain.
The Range of f is Q - {2}, which is not equal to the Co-domain Q.
Result: The function is Not Surjective (Not Onto).

Step 4: Conclusion
Since the function is one-one but not onto, it is not a bijection.

Final Answer: The function is not bijective.

Q15: Find x if \tan^{-1}{\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}}=\alpha

Solution:
Step 1: Use Substitution to Simplify
To simplify terms like \sqrt{1+x^2} and \sqrt{1-x^2}, we use trigonometric substitution.
Put x^{2} = \cos 2\theta.
Then:
\sqrt{1+x^2} = \sqrt{1+ \cos 2\theta} = \sqrt{2 \cos ^{2}\theta} = \sqrt {2}\cos \theta

\sqrt{1-x^{2}} = \sqrt{1-\cos 2\theta} = \sqrt{2\sin^{2} \theta} = \sqrt{2} \sin \theta

Step 2: Substitute into the Expression
\tan^{-1}{\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}}=\tan^{-1}{\frac{\sqrt {2}\cos \theta-\sqrt{2} \sin \theta}{\sqrt {2}\cos \theta+\sqrt{2} \sin \theta}}

\tan^{-1}{\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}}=\tan^{-1}{\frac{\cos \theta- \sin \theta}{\cos \theta+ \sin \theta}}

Step 3: Convert to Tangent Form
Divide both the numerator and denominator by \cos \theta:
\tan^{-1}{\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}}=\tan^{-1}{\frac{1- \tan \theta}{1+ \tan \theta}}

We know that \tan(\frac{\pi}{4} - \theta) = \frac{1 - \tan \theta}{1 + \tan \theta}.

So, the expression simplifies to
\tan^{-1}{\frac{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}}=\tan^{-1}{\tan(\frac{\pi}{4} - \theta)}

Step 4: Solve for the Angle
Substituting in original equation:
\tan^{-1}{\tan(\frac{\pi}{4} - \theta)} = \alpha

\frac{\pi}{4} - \theta = \alpha

\theta = \frac{\pi}{4} - \alpha

Step 5: Find x
Substituting back x^{2} = \cos 2\theta.
Substitute the value of \theta:
x^{2} = \cos 2(\frac{\pi}{4} - \alpha)

x^{2} = \cos(\frac{\pi}{2} - 2\alpha)

Using the complementary angle identity \cos(\frac{\pi}{2} - A) = \sin A:
x^{2} = \sin 2\alpha

x = \sqrt{\sin 2\alpha}

Final Answer: \boxed{x = \sqrt{\sin 2\alpha}}

Section D: 5 marks questions

Q16: A relation R is defined on a set of real numbers R as R={(x,y): x \cdot y \text{ is an irrational number}}. Check whether R is reflexive, symmetric and transitive or not.

Solution:
Step 1: Check Reflexivity
A relation is reflexive if (x, x) \in R for all x \in \mathbb{R}.
This implies x \cdot x = x^2 must always be an irrational number.
Counter-example: Let x = \sqrt{2} (which is an irrational number).
x \cdot x = \sqrt{2} \cdot \sqrt{2} = 2.
Since 2 is a rational number, (\sqrt{2}, \sqrt{2}) \notin R.
Result: R is Not Reflexive.

Step 2: Check Symmetry
A relation is symmetric if (x, y) \in R \implies (y, x) \in R.
If x \cdot y is an irrational number, then y \cdot x is the same number (commutative property of multiplication).
Therefore, y \cdot x is also irrational.
Result: R is Symmetric.

Step 3: Check Transitivity
A relation is transitive if (x, y) \in R and (y, z) \in R \implies (x, z) \in R.
Counter-example: Let x = 1 (Rational) Let y = \sqrt{2} (Irrational) Let z = 2 (Rational)

Check (x, y): 1 \cdot \sqrt{2} = \sqrt{2} (Irrational).
So, (1, \sqrt{2}) \in R.

Check (y, z): \sqrt{2} \cdot 2 = 2\sqrt{2} (Irrational).
So, (\sqrt{2}, 2) \in R.

Check (x, z): 1 \cdot 2 = 2 (Rational).
Since the product is rational, (1, 2) \notin R.

Result: R is Not Transitive.

Conclusion: The relation is only Symmetric.

Section E (Case Study): 4 marks questions (1+1+2)

Q17 (Case Study): Students of Grade 9, planned to plant saplings along straight lines, parallel to each other to one side of the playground ensuring that they had enough play area. Let us assume that they planted one of the rows of the saplings along the line 𝑦 = 𝑥 − 4. Let L be the set of all lines which are parallel on the ground and R be a relation on L.
Answer the following using the above information..

(i) Let relation R be defined by R={(L1,L2): L1 || L2}. Is R an equivalence relation?

Solution:

1. Reflexive: Every line is parallel to itself. (L1 || L1) is true. (Reflexive).
2. Symmetric: If line L1 is parallel to L2, then L2 is parallel to L1. (Symmetric).
3. Transitive: If L1 || L2 and L2 || L3, then L1 is parallel to L3. (Transitive). Answer: Yes, it is an equivalence relation.

(ii) Let R={(L1,L2): L1 \perp L2}. Check if R is Symmetric?

Solution:
If L1 is perpendicular to L2, the angle between them is 90^\circ.
Consequently, L2 is also perpendicular to L1.
Answer: Yes, R is Symmetric.

(iii) Check function f: R\rightarrow R defined by f(x)=x-4 is bijective.

Solution: This is a linear function representing a straight line.

1. One-One: Let f(x_1) = f(x_2) \implies x_1 - 4 = x_2 - 4 \implies x_1 = x_2.
2. Onto: For every real number y, there exists x = y + 4 such that f(x) = y.
   Answer: Yes, it is Bijective.

Q18 (Case Study): In a school project Sheetal was asked to construct a triangle and name it as ABC. Two angles A and B were given to be equal to \tan^{-1}\frac{1}{2} and \tan^{-1}\frac{1}{3}.

(i) Find the value of \sin A.
Solution:
Given A = \tan^{-1}\frac{1}{2}, we have \tan A = \frac{1}{2}.

In a right triangle with angle A: Opposite = 1, Adjacent = 2. Hypotenuse = \sqrt{1^2 + 2^2} = \sqrt{5}.

Therefore, \sin A = \frac{\text{Opposite}}{\text{Hypotenuse}} = \frac{1}{\sqrt{5}}.

Answer: \frac{1}{\sqrt{5}}

(ii) If B= \cos^{-1}x then find x.

Solution:
Given B = \tan^{-1}\frac{1}{3}, we have \tan B = \frac{1}{3}.

In a right triangle with angle B: Opposite = 1, Adjacent = 3. Hypotenuse = \sqrt{1^2 + 3^2} = \sqrt{10}.

We need \cos B: \cos B = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{3}{\sqrt{10}}. So, B = \cos^{-1}(\frac{3}{\sqrt{10}}).

Comparing with B = \cos^{-1}x, we get x = \frac{3}{\sqrt{10}}.

Answer: x = \frac{3}{\sqrt{10}}

(iii) Find the value of A+B.

Solution:
A + B = \tan^{-1}\frac{1}{2} + \tan^{-1}\frac{1}{3}.

Using the formula \tan^{-1}x + \tan^{-1}y = \tan^{-1}(\frac{x+y}{1-xy}):

Check product: \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6} < 1.

Sum = \tan^{-1}(\frac{\frac{1}{2} + \frac{1}{3}}{1 - \frac{1}{6}})

Numerator = \frac{3+2}{6} = \frac{5}{6}. Denominator = \frac{6-1}{6} = \frac{5}{6}.

A + B = \tan^{-1}(\frac{5/6}{5/6}) = \tan^{-1}(1).

The principal value for \tan^{-1}(1) is \frac{\pi}{4}.

Answer: \boxed{A + B = \frac{\pi}{4}}