Class 12 Full Syllabus Practice Paper-1 2026 ⇒
Section A (1 mark each)
Q1: The sum of n terms of the sequence given by a_{n}=5-6n, where n \in N is:
a) 5-6n
b) 2-3n
c) n(2-3n)
d) None of these
Solution:
Step 1: Identify the nature of the sequence The given general term is linear in n.
Any sequence where the n^{th} term is a linear expression in n (of the form An + B) is an Arithmetic Progression (A.P.).
Given: a_{n} = 5 - 6n
Step 2: Find the first term (a) and the common difference (d)
To find the first term (a), substitute n = 1 into the general term equation:
a = a_{1} = 5 - 6(1) = 5 - 6 = -1
To find the second term, substitute n = 2:
a_{2} = 5 - 6(2) = 5 - 12 = -7
Now, find the common difference (d):
d = a_{2} - a_{1} = -7 - (-1) = -6
(Teacher’s Note: In a linear equation a_n = An + B, the coefficient of n is always the common difference. Here, the coefficient is -6, so d = -6.)
Step 3: Apply the Sum of n terms formula
The formula for the sum of n terms (S_n) of an A.P. is:
S_{n} = \frac{n}{2}[2a + (n-1)d]
Substitute the values we found (a = -1 and d = -6):
S_{n} = \frac{n}{2} [2(-1) + (n-1)(-6)]
Step 4: Simplify the expression
S_{n} = \frac{n}{2} [-2 - 6n + 6]
S_{n} = \frac{n}{2} [4 - 6n]
S_{n} = \frac{n}{2} \times 2[2 - 3n]
S_{n} = n(2 - 3n)
Correct Option: (C)
Alternative Short Method (Teacher’s Tip)
Since you know the first term (a = -1) and the last term (l = a_n = 5-6n), you can use the shorter formula:
S_{n} = \frac{n}{2}(a+l)
S_{n} = \frac{n}{2}(-1 + 5 - 6n)
S_{n} = \frac{n}{2}(4 - 6n)
S_{n} = n(2 - 3n)
Q2: The length of the foot of the perpendicular from the point P(3,4,5) on Y axis is
a) 10
b) \sqrt{34}
c) \sqrt{113}
d) 5\sqrt{2}
Solution:
Step 1: Understand coordinates on the Y-axis
If we drop a perpendicular from any point P(x, y, z) to the Y-axis, the foot of the perpendicular will lie on the Y-axis.
On the Y-axis, the x-coordinate and z-coordinate are always zero.
Thus, the coordinates of the foot of the perpendicular M will be (0, y, 0).
Step 2: Determine the coordinates of the foot of the perpendicular
Given point P(3, 4, 5).
The foot of the perpendicular M on the Y-axis will have the same y-coordinate as P, while x and z will be 0.
So, M = (0, 4, 0).
Step 3: Calculate the length of the perpendicular (Distance PM)
We need to find the distance between P(3, 4, 5) and M(0, 4, 0) using the distance formula:
d = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 }
Substitute the values:
d = \sqrt{ (3 - 0)^2 + (4 - 4)^2 + (5 - 0)^2 }
PM = \sqrt{(3)^2 + 0 + (5)^2}
PM = \sqrt{9 + 25}
PM = \sqrt{34}
Correct Option: (b)
Q3: Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are respectively
a) 4, 7
b) 7, 4
c) 4, 4
d) 7, 7
Solution:
Step 1: Use the formula for the number of subsets
If a set has k elements, the total number of subsets is 2^k.
Let the first set have m elements.
Its number of subsets is 2^m.
Let the second set have n elements.
Its number of subsets is 2^n.
Step 2: Set up the equation from the given condition
The problem states that the number of subsets of the first set is 112 more than the second.
2^m - 2^n = 112
Step 3: Solve for m and n by factoring
We can factor out 2^n from the equation (assuming m > n):
2^n (2^{m-n} - 1) = 112
Now, find factors of 112 that are powers of 2.
112 = 16 \times 7
112 = 2^4 \times 7
So, we can equate:
2^n (2^{m-n} - 1) = 2^4 \times 7
Comparing the terms:
2^n = 2^4 \Rightarrow n = 4
2^{m-n} - 1 = 7
2^{m-4} - 1 = 7
2^{m-4} = 8
2^{m-4} = 2^3
Comparing powers
m-4 = 3
m = 7
Thus, m = 7 and n = 4.
Correct Option: (b)
Q4: How many 4-digit numbers can be formed using the digits 1 to 9, if repetition of digits is not allowed?
a) 3024
b) 3026
c) 3040
d) 3014
Solution:
Step 1: Identify the available digits and positions
We have 9 distinct digits: 1, 2, 3, 4, 5, 6, 7, 8, 9. We need to form a 4-digit number, which means filling 4 distinct places: Thousands, Hundreds, Tens, and Ones.
Step 2: Apply the Fundamental Principle of Counting (Permutations)
Since repetition is not allowed, we select and arrange 4 digits out of 9.
This is a permutation problem denoted as ^9P_4.
^9P_4 = \frac{9!}{(9-4)!}
^9P_4 = \frac{9!}{5!}
^9P_4 = 9 \times 8 \times 7 \times 6
^9P_4 = 3024
Alternatively, think of the places:
- Thousands place: 9 options
- Hundreds place: 8 options (one used)
- Tens place: 7 options (two used)
- Ones place: 6 options (three used) Total = 9 \times 8 \times 7 \times 6 = 3024.
Correct Option: (a)
Q5: If (1-i)^{4}=a+ib then the value of a and b are respectively
a) -4, 0
b) 0, -4
c) 4, 0
d) 0, 4
Solution:
Step 1: Simplify the complex number expression
We need to compute (1-i)^4. It is easier to calculate (1-i)^2.
First, calculate (1-i)^2 using the identity (a-b)^2 = a^2 - 2ab + b^2:
(1-i)^2 = 1^2 - 2(1)(i) + i^2
(1-i)^2 = 1 - 2i - 1
(1-i)^2 = -2i
Step 2: Square the result to find the 4th power
Now, substitute this back: (1-i)^4 = (-2i)^2
(1-i)^4 = (-2)^2 \times i^2
(since i^2 = -1)
(1-i)^4 = 4 \times (-1)
(1-i)^4 = -4
Step 3: Compare with a+ib
We found (1-i)^4 = -4.
This can be written in complex form as: -4 + 0i
Comparing with a + ib:
a = -4
b = 0
Correct Option: (a)
Q6: The slope of the lines which makes equal intercept with the axis is
a) 1
b) -1
c) 2
d) 4
Solution:
Step 1: Write the intercept form of a line
The equation of a line with x-intercept a and y-intercept b is:
\frac{x}{a} + \frac{y}{b} = 1
Step 2: Apply the “equal intercepts” condition
The problem states the line makes “equal intercepts”. This implies a = b (both in magnitude and sign, typically, though magnitude alone usually gives \pm 1).
If we assume a = b:
\frac{x}{a} + \frac{y}{a} = 1
x + y = a
Step 3: Find the slope
Convert x + y = a into slope-intercept form (y = mx + c):
y = -x + a
Here, the coefficient of x is the slope m.
m = -1
Correct Option: (b)
Q7: The point (-4, -3, -5) lies in
a) I Octant
b) VII Octant
c) V Octant
d) III Octant
Solution:
Step 1: Analyze the signs of the coordinates
The given point is P(-4, -3, -5).
- x-coordinate is negative (-)
- y-coordinate is negative (-)
- z-coordinate is negative (-)
Step 2: Match the sign convention to the Octants
In 3D geometry, the octants are determined by the signs of (x, y, z):
- I: (+, +, +)
- V: (+, +, -) (z is negative)
- VII: (-, -, -) (All negative)
Since our point has signs (-, -, -), it lies in the VII Octant.
Correct Option: (b)
Q8: The nth term of a GP 5, 25, 125, … is
a) 5^{n}
b) 5^{n-1}
c) 5^{n+1}
d) 5^{n-2}
Solution:
Step 1: Identify the First Term and Common Ratio
The given Geometric Progression (GP) is: 5, 25, 125…
First term (a) = 5
Common ratio (r) = \frac{25}{5} = 5
Step 2: Apply the formula for the nth term
The general term of a GP is given by:
a_n = a \cdot r^{n-1}
Substitute a = 5 and r = 5:
a_n = 5 \cdot 5^{n-1}
Step 3: Simplify using exponent rules
Using the rule x^m \cdot x^n = x^{m+n}:
a_n = 5^1 \cdot 5^{n-1}
a_n = 5^{1+n-1}
a_n = 5^{n }
Correct Option: (a)
Q9: If \frac{1}{8!}+\frac{1}{9!}=\frac{x}{10!} then find the value of x
a) 90
b) 100
c) 80
d) 95
Solution:
Step 1: Eliminate the denominators
To simplify, multiply the entire equation by the largest factorial present, which is 10!.
10! \times [\frac{1}{8!}+\frac{1}{9!}] = 10! \times \frac{x}{10!}
Step 2: Expand the factorials
\frac{10!}{8!}+\frac{10!}{9!}] = x
Recall that 10! = 10 \times 9 \times 8! and 10! = 10 \times 9!.
(10 \times 9) + 10 = x
Step 3: Solve for x
90 + 10 = x
x = 100
Correct Option: (b)
Q10: Given ordered pair is (2a - 5, 4)=(5, b+6). The values of a and b are
a) -2, 5
b) 2, 5
c) 5, 2
d) 5, -2
Solution:
Step 1: Equate corresponding components
Two ordered pairs are equal if their corresponding first and second elements are equal.
x-component: 2a - 5 = 5
y-component: 4 = b + 6
Step 2: Solve for a
2a = 5 + 5
2a = 10
a = 5
Step 3: Solve for b
b = 4 - 6
b = -2
So, a = 5 and b = -2.
Correct Option: (d)
Q11: The income of a person is Rs. 3,00,000 in the first year and he receives an increase of Rs. 10,000 to his income per year for the next 19 years. Find the total amount he received in 20 years.
a) 7,90,000
b) 85,00,000
c) 8,50,000
d) 79,00,000
Solution:
Step 1: Identify this as an Arithmetic Progression (AP)
The income increases by a constant amount each year, forming an AP.
First term (a) = 3,00,000
Common difference (d) = 10,000
Number of years (n) = 20
Step 2: Apply the Sum of AP formula
We need the total amount received, which is S_{20}.
S_n = \frac{n}{2} [2a + (n-1)d]
Step 3: Substitute and Calculate
S_{20} = \frac{20}{2} [2(3,00,000) + (20-1)(10,000)]
S_{20} = 10 [6,00,000 + 19(10,000)]
S_{20} = 10 [6,00,000 + 1,90,000]
S_{20} = 10 [7,90,000]
S_{20} = 79,00,000]
Correct Option: (d)
Q12: A card is drawn at random from a well shuffled pack of 52 cards. Find the probability that it is either a king or a spade.
a) \frac{19}{51}
b) \frac{15}{52}
c) \frac{16}{52}
d) \frac{17}{52}
Solution:
Step 1: Define the events
Let K be the event of drawing a King.
Let S be the event of drawing a Spade.
We need to find P(K \cup S) (King OR Spade).
Step 2: Identify the probabilities
Total cards = 52
Number of Kings n(K) = 4 (Hearts, Diamonds, Clubs, Spades)
Number of Spades n(S) = 13
Number of cards that are both King and Spade n(K \cap S) = 1 (The King of Spades)
Step 3: Apply the Addition Theorem of Probability
P(K \cup S) = P(K) + P(S) - P(K \cap S)
P(K \cup S) = \frac{4}{52} + \frac{13}{52} - \frac{1}{52}
(Teacher’s Note: We subtract P(K \cap S) because the King of Spades was counted twice—once in the Kings group and once in the Spades group.)
Step 4: Calculate the final probability
P(K \cup S) = \frac{4 + 13 - 1}{52}
P(K \cup S) = \frac{16}{52}
Correct Option: (c)
Q13: Compute the derivative of f(x)=\sin^{2}x
a) \cos {2x}
b) 2\sin x
c) \sin {2x}
d) \cos^{2}x
Solution:
Step 1: Apply the Chain Rule
Let f(x) = (\sin~x)^2.
To differentiate this, we apply the chain rule: \frac{d}{dx}[u^n] = n \cdot u^{n-1} \cdot \frac{du}{dx}.
Here, u = \sin~x and n = 2.
f'(x) = 2 \cdot (\sin~x)^{2-1} \cdot \frac{d}{dx}(\sin~x)
Step 2: Differentiate the inner function
The derivative of \sin~x is \cos~x.
f'(x) = 2 \cdot \sin~x \cdot \cos~x
Step 3: Use the double angle identity
Recall the trigonometric identity: \sin~2A = 2~\sin~A~\cos~A. Therefore:
f'(x) = \sin~2x
Correct Option: (c)
Q14: Find the derivative of f(x)=1+x+x^{2}+x^{3}+...+x^{50} at x=1.
a) 1225
b) 1500
c) 1375
d) 1275
Solution:
Step 1: Differentiate the function term by term
Using the power rule \frac{d}{dx}(x^n) = nx^{n-1}:
f'(x) = \frac{d}{dx}(1) + \frac{d}{dx}(x) + \frac{d}{dx}(x^2) + ... + \frac{d}{dx}(x^50)
f'(x) = 0 + 1 + 2x + 3x^2 + ... + 50x^{49}
Step 2: Substitute x=1 into the derivative
f'(1) = 1 + 2(1) + 3(1)^2 + ... + 50(1)^{49}
f'(1) = 1 + 2 + 3 + ... + 50
Step 3: Calculate the sum of the series
This is the sum of the first 50 natural numbers.
The formula for the sum of the first n natural numbers is:
S_n = \frac{n(n+1)}{2}
Here, n = 50:
S_{50} = \frac{50(50+1)}{2}
S_{50} = \frac{50 \times 51}{2}
S_{50} = 25 \times 51
S_{50} = 1275
Correct Option: (d)
Q15: Find the radius of the circle x^{2}+y^{2}+8x+10y-8=0.
a) 7
b) 10
c) 15
d) 11
Solution:
Step 1: Compare with the general equation of a circle
The general equation is x^2 + y^2 + 2gx + 2fy + c = 0.
Comparing this with the given equation x^2 + y^2 + 8x + 10y - 8 = 0:
2g = 8 \Rightarrow g = 4
2f = 10 \Rightarrow f = 5
c = -8
Step 2: Apply the radius formula
The radius r is given by:
r = sqrt{g^2 + f^2 - c}
Step 3: Calculate the value
r = sqrt{4^2 + 5^2 -(-8)}
r = \sqrt{16 + 25 + 8}
r = \sqrt{49}
r = 7
Correct Option: (a)
Q16: lim_{x\rightarrow0}\frac{x^{2}\cos~x}{1-\cos~x} is
a) 2
b) \frac{3}{2}
c) \frac{-3}{2}
d) 1
Solution:
Step 1: Simplify the expression using rationalization or identities
We can multiply the numerator and denominator by the conjugate (1 + \cos~x):
L = lim_{x\rightarrow0}\frac{x^{2}\cos~x(1+\cos~x)}{(1-\cos x)(1+\cos x)}
L = lim_{x\rightarrow0}\frac{x^{2}\cos~x(1+\cos~x)}{1-\cos^{2}x}
Step 2: Use trigonometric identities
Since 1 - \cos^2x = \sin^2x:
L = lim_{x\rightarrow0}\frac{x^{2}\cos~x(1+\cos~x)}{\sin^{2}x}
Group the terms to use the standard limit lim_{x\rightarrow0}\frac{x}{sin~x} = 1:
L = lim_{x\rightarrow0} \left(\frac{x}{\sin x} \right)^2 \cdot \cos~x(1+\cos~x)
Step 3: Evaluate the limit
L = 1 \cdot \cos~0(1+\cos~0)
L = 1 \cdot 1(1+1)
L = 1 \cdot 1 \cdot 2 = 2
Correct Option: (a)
Q17: If the first term and common ratio of a GP are 1 and 3 respectively, then find the sum of its third and fifth term.
a) 70
b) 80
c) 90
d) 100
Solution:
Step 1: Identify the GP parameters
First term (a) = 1
Common ratio (r) = 3
Step 2: Find the 3rd and 5th terms
The general term of a GP is a_n = ar^{n-1}.
Third term (a_3):
a_3 = 1 \cdot (3)^{3-1} = 3^2 = 9.
Fifth term (a_5):
a_5 = 1 \cdot (3)^{5-1} = 3^4 = 81.
Step 3: Calculate the sum Sum = a_3 + a_5 Sum = 9 + 81 Sum = 90
Correct Option: (C)
Q18: Events E and F are such that P (not E or not F) = 0.25.
a) E and F are mutually exclusive events.
b) E and F are not mutually exclusive events.
c) E and F are Exhaustive
d) None of these
Solution:
Step 1: Understand “not E or not F”
Using De Morgan’s Law from Set Theory, “not E or not F” is equivalent to “not (E and F)”.
In probability notation: P(\bar{E} \cup \bar{F}) = P(\overline{E \cap F})
Step 2: Use the complement rule
We know that P(\bar{A}) = 1 - P(A).
So, P(\overline{E \cap F}) = 1 - P(E \cap F)
Given in the question:
1 - P(E \cap F) = 0.25
Step 3: Calculate P(E \cap F)
P(E \cap F) = 1 - 0.25
P(E \cap F) = 0.75
Step 4: Check for Mutually Exclusive condition
Two events are mutually exclusive if they cannot happen at the same time, meaning their intersection probability P(E \cap F) must be 0.
Here, P(E \cap F) = 0.75, which is not equal to 0.
Therefore, E and F are not mutually exclusive.
Correct Option: (B)
Q19: Suppose A and B are two events such that P(A)=0.54, P(B)=0.69 and P(A \cup B)=0.88. Find P(A \cap B).
a) 0.35
b) 0.20
c) 0.30
d) None of these
Solution:
Step 1: Apply the General Addition Rule
The formula relating union and intersection is:
P(A \cup B) = P(A) + P(B) - P(A \cap B)
Step 2: Substitute the known values
0.88 = 0.54 + 0.69 - P(A \cap B)
Step 3: Solve for P(A \cap B)
0.88 = 1.23 - P(A \cap B)
P(A \cap B) = 1.23 - 0.88
P(A \cap B) = 0.35
Correct Option: (A)
Q20: Express 50^{\circ}37^{\prime}30^{\prime\prime} in radian
a) \frac{7\pi}{32}
b) \frac{5\pi}{32}
c) \frac{9\pi}{32}
d) \frac{\pi}{32}
Solution:
Step 1: Convert Seconds to Minutes
We know that 60^{\prime\prime} = 1^{\prime}.
So, 30^{\prime\prime} = \frac{30}{60}^{\prime} = 0.5^{\prime}
Add this to the minutes part:
37^{\prime} + 0.5^{\prime} = 37.5^{\prime}
Step 2: Convert Minutes to Degrees
We know that 60^{\prime} = 1^{\circ}.
So, 37.5^{\prime} = \frac{37.5}{60}^{\circ}
\frac{37.5}{60} = \frac{375}{600} = \frac{5}{8}^{\circ} = 0.625^{\circ}
Step 3: Combine to get total degrees
Total angle = 50^{\circ} + 0.625^{\circ} = 50.625^{\circ} Converting to improper fraction:
50\frac{5}{8} = \frac{50 \times 8 + 5}{8} = \frac{405}{8}^{\circ}
Step 4: Convert Degrees to Radians
To convert degrees to radians, multiply by \frac{\pi}{180}.
\text{Radian measure} = \frac{405}{8} \times \frac{\pi}{180}
\text{Radian measure} = \frac{9}{8} \times \frac{\pi}{4}
\text{Radian measure} = \frac{9\pi}{32}
Correct Option: (C)
Section B (2 marks each)
Q21: A die is loaded on such a way that each odd number is twice as likely to occur as even number. Find P(G), where G is an event that a number greater than 3 occurs on a single roll of the die.
Solution:
Step 1: Define the probabilities for odd and even numbers
Let the probability of an even number occurring be x.
Since odd numbers are twice as likely, the probability of an odd number occurring is 2x.
Probability of Even numbers {2, 4, 6}: P(2) = P(4) = P(6) = x
Probability of Odd numbers {1, 3, 5}: P(1) = P(3) = P(5) = 2x
Step 2: Find the value of x
The sum of probabilities of the sample space S = {1, 2, 3, 4, 5, 6} must be 1.
P(1) + P(2) + P(3) + P(4) + P(5) + P(6) = 1
2x + x + 2x + x + 2x + x = 1
9x = 1
x = \frac{1}{9}
So, P(\text{Even}) = \frac{1}{9} and P(\text{Odd}) = \frac{2}{9}.
Step 3: Identify Event G and calculate its probability
Event G is getting a number greater than 3.
G = {4, 5, 6}
P(G) = P(4) + P(5) + P(6)
Substitute the values:
- 4 is Even \rightarrow P(4) = \frac{1}{9}
- 5 is Odd \rightarrow P(5) = \frac{2}{9}
- 6 is Even \rightarrow P(6) =\frac{1}{9}
P(G) = \frac{1}{9} + \frac{2}{9} + \frac{1}{9}
P(G) = \frac{4}{9}
Answer: \boxed{ P(G) = \frac{4}{9}}
Q22: If L={1,2,3,4}, M={3,4,5,6} and N={1,3,5}, then verify that L-(M \cup N) = (L-M) \cap (L-N).
Solution:
Step 1: Solve the Left Hand Side (LHS)
First, find M \cup N (Union of M and N):
M \cup N = {1, 3, 4, 5, 6}
Now find L - (M \cup N) (Elements in L that are not in the union):
L = {1, 2, 3, 4}
Removing 1, 3, and 4 from L:
L - (M \cup N) = {2}
LHS = {2}
Step 2: Solve the Right Hand Side (RHS)
First, find L - M (Elements in L not in M): L - M = {1, 2} (Removed 3, 4)
Next, find L - N (Elements in L not in N): L - N = {2, 4} (Removed 1, 3)
Now find the intersection:
RHS = (L - M) \cap (L - N)
RHS = {1, 2} \cap {2, 4}
RHS = {2}
Step 3: Conclusion Since LHS = {2} and RHS = {2}:
[Latex] LHS = RHS [/latex]
Hence Verified \boxed{ L-(M \cup N) = (L-M) \cap (L-N)}
Q23: Find the derivative of \frac{\sin~x+\cos~x}{\sin~x-\cos~x} with respect to x.
Solution:
Step 1: Apply the Quotient Rule
Let y = \frac{u}{v}, where u = \sin~x + \cos~x and v = \sin~x - \cos~x.
The quotient rule is: \frac{dy}{dx} = \frac{v \cdot u' - u \cdot v'}{v^2}
Step 2: Find the derivatives of u and v
u' = \frac{d}{dx}(\sin~x + \cos~x) = \cos~x - \sin~x
v' = \frac{d}{dx}(\sin~x - \cos~x) = \cos~x - (-\sin~x) = \cos~x + \sin~x
Step 3: Substitute into the formula
\frac{dy}{dx} = \frac{(\sin~x - \cos~x)(\cos~x - \sin~x) - (\sin~x + \cos~x) (\cos~x + \sin~x)}{(\cos~x + \sin~x)^2}
Step 4: Simplify the Numerator
Notice that (\sin~x - \cos~x) = -(\cos~x - \sin~x).
So, the first term is -(\cos~x - \sin~x)^2.
The second term is -(\sin~x + \cos~x)^2.
Numerator = -[ (\cos~x - \sin~x)^2 + (\sin~x + \cos~x)^2 ]
Expand both squares:
(\cos~x - \sin~x)^2 = \cos^2x + \sin^2x - 2\sin~x~\cos~x = 1 - \sin~2x
(\sin~x + \cos~x)^2 = \sin^2x + \cos^2x + 2\sin~x~\cos~x = 1 + \sin~2x
Numerator = -[ (1 - \sin~2x) + (1 + \sin~2x) ]
Numerator = -[ 2 ] = -2
Step 5: Final Result
\frac{dy}{dx} = \frac{-2}{(\sin~x + \cos~x)^2}
(Alternative Answer Form: \frac{-2}{1 - \sin~2x})
Final Answer: \boxed { \frac{dy}{dx} = \frac{-2}{(\sin~x + \cos~x)^2}}
Here are the step-by-step solutions for Questions 24 to 26, formatted for your WordPress Gutenberg editor.
Q24: Find r, if 5P_{r}^{4}=6P_{r-1}^{5}
Solution:
Step 1: Writing the equation
5 \cdot ^4P_{r}=6 \cdot ^5P_{r-1}
Step 2: Expand using the Permutation Formula
The formula for ^nP_r is \frac{n!}{(n-r)!}.
LHS: 5 \times \frac{4!}{(4-r)!}
RHS: 6 \times \frac{5!}{(5-(r-1))!} = 6 \times \frac{5!}{(6-r)!}
Substituting in equation:
5 \times \frac{4!}{(4-r)!} = 6 \times \frac{5!}{ (6-r)! }
Step 3: Simplify the factorials
We know that 5! = 5 \times 4!.
Substitute this into the RHS:
5 \times \frac{4!}{(4-r)!} = 6 \times \frac{5 \times 4!}{(6-r)!}
\frac{1}{(4-r)!} = \frac{6}{(6-r)!}
Step 4: Expand the denominator to cancel terms
We know that (6-r)! = (6-r)(5-r)(4-r)!.
Substitute this into the equation:
\frac{1}{(4-r)!} = \frac{6}{(6-r)(5-r)(4-r)!}
\frac{1}{1} = \frac{6}{(6-r)(5-r)}
Step 5: Solve the quadratic equation
Cross multiply:
(6-r)(5-r) = 6
30 - 6r - 5r + r^2 = 6
r^2 - 11r + 30 = 6
r^2 - 11r + 24 = 0
Factorize the quadratic equation: (r-8)(r-3) = 0
So, r = 8 or r = 3.
Step 6: Check the validity of r
In ^nP_r, r must be less than or equal to n.
For ^4P_r, we must have r \le 4.
Therefore, r = 8 is rejected.
Final Answer: \boxed{r = 3}
Q25: Prove that \frac{\cos~7x+\cos~5x}{\sin~7x-\sin~5x}=\cot~x
Solution:
Step 1: Apply Trigonometric Transformation Formulas
We need to convert sums to products.
- Numerator (Cos C + Cos D) = 2~\cos(\frac{C+D}{2})~\cos(\frac{C-D}{2})
- Denominator (Sin C – Sin D) = 2~\cos(\frac{C+D}{2})~\sin(\frac{C-D}{2})
Here, C = 7x and D = 5x.
Step 2: Substitute into the expression
Numerator:
\cos 7x + \cos 5x = 2 \cos(\frac{7x+5x}{2}) \cos(\frac{7x - 5x}{2})
\cos 7x + \cos 5x = 2 \cos(6x) \cos(x)
Denominator:
\sin 7x - \sin 5x = 2 \cos(\frac{7x+5x}{2}) \sin(\frac{7x -5x}{2})
\sin 7x - \sin 5x = 2~cos(6x)~sin(x)
Step 3: Simplify the fraction
LHS = \frac{2 \cos(6x) \cos(x)}{2 \cos(6x) \sin(x)}
LHS = \frac{\cos(x)}{\sin(x)}
LHS = \cot x = RHS
Hence Proved.
Q26(A): Are the points A(3,6,9), B(10, 20, 30) and C(25,-41,5) the vertices of a right angled triangle?
Solution
Step 1: Calculate the squared lengths of the sides
Using the distance formula d^2 = (x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2:
Side AB^2:
AB^2 = (10-3)^2 + (20-6)^2 + (30-9)^2
AB^2 = 7^2 + 14^2 + 21^2 = 49 + 196 + 441 = 686
Side BC^2:
BC^2 = (25-10)^2 + (-41-20)^2 + (5-30)^2
BC^2 = 15^2 + (-61)^2 + (-25)^2 = 225 + 3721 + 625 = 4571
Side AC^2:
AC^2 = (25-3)^2 + (-41-6)^2 + (5-9)^2
AC^2 = 22^2 + (-47)^2 + (-4)^2 = 484 + 2209 + 16 = 2709
Step 2: Check Pythagoras Theorem
For a right-angled triangle, the sum of the squares of the two smaller sides must equal the square of the largest side.
Smaller sides: AB^2 and AC^2.
AB^2 + AC^2 = 686 +2079 = 3395
Compare with the largest side BC^2:
3395 \neq 4571
AB^2 + AC^2 \neq BC^2
Conclusion: No, the points do not form a right-angled triangle.
Q26(B): Three vertices of a parallelogram ABCD are A(3,-1,2), B(1,2,-4) and C(-1,1,2). Find the coordinates of the fourth vertex.
Solution:
Step 1: Use the Midpoint Property of a Parallelogram
In a parallelogram, the diagonals bisect each other.
This means the midpoint of diagonal AC is the same as the midpoint of diagonal BD.
Step 2: Find the midpoint of AC
Let M be the midpoint of AC.
M = (\frac{3 + (-1)}{2}, \frac{-1 + 1}{2}, \frac{2+2}{2})
M = (\frac{2}{2}, \frac{0}{2}, \frac{4}{2})
M = (1, 0, 2)
Step 3: Find the fourth vertex D(x, y, z)
The midpoint of BD (joining B(1,2,-4) and D(x,y,z)) must also be (1, 0, 2).
For x: \frac{1+x}{2} = 1 \Rightarrow 1+x = 2 \Rightarrow x = 1
For y: \frac{2+y}{2} = 0 \Rightarrow 2+y = 0 \Rightarrow y = -2
For z: \frac{-4+z}{2} = 2 \Rightarrow -4+z = 4 \Rightarrow z = 8
Final Answer: The coordinates of the fourth vertex D are (1, -2, 8).
Here are the step-by-step solutions for Section C: Questions 27 to 31, formatted for your WordPress Gutenberg editor.
Section C (3 marks each)
Q27: Find the variance of the given data.
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 5 | 8 | 15 | 16 | 6 |
Solution:
Step 1: Create a table to calculate Mean and Variance
We need the class mark (x_i) of the classes and the product f_i x_i to find the mean (\bar{x}).
| Class | Frequency (f_i) | Midpoint (x_i) | f_i x_i | x_i - \bar{x} | (x_i - \bar{x})^2 | f_i(x_i - \bar{x})^2 |
| 0-10 | 5 | 5 | 25 | -22 | 484 | 2420 |
| 10-20 | 8 | 15 | 120 | -12 | 144 | 1152 |
| 20-30 | 15 | 25 | 375 | -2 | 4 | 60 |
| 30-40 | 16 | 35 | 560 | 8 | 64 | 1024 |
| 40-50 | 6 | 45 | 270 | 18 | 324 | 1944 |
| Total | N = 50 | 1350 | 6600 |
Step 2: Calculate the Mean (\bar{x})
\bar{x} = \frac{\sum f_i x_i}{N}
\bar{x} = \frac{1350}{50} = 27
Step 3: Calculate the Variance (\sigma^2)
The formula for variance is:
\sigma^2 = \frac{\sum f_i(x_i - \bar{x})^2}{N}
Using the sum from the table:
\sigma^2 = \frac{6600}{50}
\sigma^2 = 132
Answer: \boxed{ \text{Variance } = 132}
Q28: Find the domain and range of the real function \sqrt{9-x^{2}}
Solution:
Step 1: Find the Domain
For the square root function f(x) = \sqrt{9-x^2} to be defined in real numbers, the expression inside the root must be non-negative.
9 - x^2 \ge 0
x^2 \le 9
Taking the square root of both sides:
|x| \le 3
This implies:
-3 \le x \le 3
Domain: [-3, 3]
Step 2: Find the Range
Let y = \sqrt{9-x^2}.
Since \sqrt{} always yields a non-negative result:
y \ge 0 … (i)
Also, since x^2 \ge 0, the maximum value of 9-x^2 is 9 (when x=0).
Therefore, the maximum value of y is \sqrt{9} = 3.
y \le 3 … (ii)
Combining (i) and (ii):
0 \le y \le 3
Range: [0, 3]
Q29: Find the equation of the line passing through the intersection of the lines 3x+y-9=0 and 4x+3y-7=0 and perpendicular to the line 5x-4y+1=0.
Solution:
Step 1: Find the point of intersection
Solve the system of equations:
3x + y = 9 \Rightarrow y = 9 - 3x
4x + 3y = 7
Substitute (1) into (2):
4x + 3(9 - 3x) = 7
4x + 27 - 9x = 7
-5x = 7 - 27
-5x = -20 \Rightarrow x = 4
Find y:
y = 9 - 3(4) = 9 - 12 = -3
Intersection Point: (4, -3)
Step 2: Find the slope of the required line
The given line is 5x - 4y + 1 = 0.
Slope m_1 = \frac{-A}{B} = \frac{-5}{-4} = \frac{5}{4}.
Since the required line is perpendicular, its slope m_2 is the negative reciprocal of m_1:
m_2 = \frac{-1}{m_1} = \frac{-1}{5/4} = \frac{-4}{5}
Step 3: Write the equation of the line
Using the Point-Slope form y - y_1 = m(x - x_1) with point (4, -3) and slope \frac{-4}{5}:
y - (-3) = \frac{-4}{5}(x - 4)
5(y + 3) = -4(x - 4)
5y + 15 = -4x + 16
4x + 5y - 1 = 0
Final Answer: \boxed{ 4x + 5y - 1 = 0}
Q30: Evaluate lim_{x\rightarrow0}\frac{\tan~x-\sin~x}{x^{3}}
Solution:
Step 1: Simplify the trigonometric expression
\tan x - \sin x = \frac{\sin x}{\cos x} - \sin x
Factor out \sin x:
= \sin x (\frac{1}{\cos x} - 1)
= \sin x (\frac{1 - \cos x}{\cos x})
Step 2: Rewrite the limit
L = \lim_{x\rightarrow0} \frac{\sin x (1 - \cos x)}{x^3 \cos x}
Step 3: Group terms with standard limits
We know standard limits:
\lim_{x\rightarrow0} \frac{\sin x}{x} = 1
\lim_{x\rightarrow0} \frac{1 - \cos x}{x^2} = \frac{1}{2}
Rewrite the expression to match these forms:
L = \lim_{x\rightarrow0} \left[ (\frac{\sin x}{x}) \cdot (\frac{1 - \cos x}{x^2}) \cdot (\frac{1}{\cos x}) \right]
Step 4: Evaluate the limit
L = (1) \cdot (\frac{1}{2}) \cdot (\frac{1}{\cos 0})
L = 1 \cdot \frac{1}{2} \cdot 1
L = \frac{1}{2}
Final Answer: \boxed{ lim_{x\rightarrow0}\frac{\tan~x-\sin~x}{x^{3}} = \frac{1}{2}}
Q31: Insert three numbers between 1 and 256 so that the resulting sequence is a G.P.
Solution:
Step 1: Set up the Geometric Progression (G.P.)
Let the three numbers be G_1, G_2, G_3.
The sequence becomes: 1, G_1, G_2, G_3, 256.
First term (a) = 1
Last term (b) = 256
Total number of terms (n) = 5 (2 given + 3 inserted)
Step 2: Find the common ratio (r)
The formula for the last term is a_n = a r^{n-1}.
256 = 1 \cdot r^{5-1}
256 = r^4
We know that 4^4 = 256.
So, r = 4.
Step 3: Calculate the three numbers
G_1 = a \cdot r = 1 \cdot 4 = 4
G_2 = a \cdot r^2 = 1 \cdot 16 = 16
G_3 = a \cdot r^3 = 1 \cdot 64 = 64
Final Answer: The three numbers are \boxed{ 4, 16 \text{ and } 64 }
Section D (5 marks each)
Q32 (A): In a triangle ABC, prove that \cos^{2}\frac{A}{2}+\cos^{2}\frac{B}{2}+\cos^{2}\frac{C}{2}=2(1+\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2})
Solution:
Step 1: Use the half-angle power reduction formula
We know that \cos^2 \theta = \frac{1 + \cos~2\theta}{2}.
Applying this to the LHS:
LHS = \frac{1+\cos~A}{2} + \frac{1+\cos~B}{2} + \frac{1+\cos~C}{2}
LHS = \frac{3}{2} + \frac{1}{2}(\cos~A + \cos~B + \cos~C)
Step 2: Apply the conditional identity for sum of cosines
In a triangle ABC (where A+B+C = \pi):
(cos~A + cos~B) + cos~C
2\cos(\frac{A+B}{2})\cos(\frac{A-B}{2}) + \cos C
Utilize the Triangle Angle Sum Property
Since A + B + C = \pi, we have A + B = \pi - C.
Dividing by 2:
\frac{A+B}{2} = \frac{\pi}{2} - \frac{C}{2}
Substitute this into the cosine term:
\cos(\frac{A+B}{2}) = \cos(\frac{\pi}{2} - \frac{C}{2}) = \sin\frac{C}{2}
Now the expression becomes:
2\sin\frac{C}{2}\cos(\frac{A-B}{2}) + \cos C
Apply Half-Angle formula to the third term
Recall: cos~C = 1 - 2sin^2\frac{C}{2}
Substitute this into the expression:
2\sin\frac{C}{2}\cos(\frac{A-B}{2}) + (1 - 2sin^2\frac{C}{2})
1 + 2\sin\frac{C}{2}\cos(\frac{A-B}{2}) - 2sin^2\frac{C}{2}
1 + 2\sin\frac{C}{2} [\cos(\frac{A-B}{2}) - sin\frac{C}{2}]
We know sin\frac{C}{2} = cos(\frac{A+B}{2}) (from above). Substitute this back into the bracket:
1 + 2\sin\frac{C}{2} [\cos(\frac{A-B}{2}) - cos(\frac{A+B}{2})]
1 + 2\sin\frac{C}{2} [-2\sin(\frac{(A-B)+(A+B)}{4}) \sin(\frac{(A-B)-(A+B)}{4})]
1 + 2\sin\frac{C}{2} [-2\sin(\frac{A}{2}) \sin(\frac{-B}{2})]
1 + 2\sin\frac{C}{2} [2\sin(\frac{A}{2}) \sin(\frac{B}{2})]
1 + 4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}
\cos~A + \cos~B + \cos~C = 1 + 4\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}
Step 3: Substitute the identity back into the equation
LHS = \frac{3}{2} + \frac{1}{2} \left[ 1 + 4sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2} \right]
LHS = \frac{3}{2} + \frac{1}{2} + 2sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}
Step 4: Simplify
LHS = \frac{4}{2} + 2sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}
LHS = 2 + 2sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2}
LHS = 2 \left( 1 + sin\frac{A}{2}sin\frac{B}{2}sin\frac{C}{2} \right)
LHS = RHS
Hence Proved.
Q32(B): If \alpha and \beta are the roots of the equation a~\cos~\theta+b~\sin~\theta=c, show that \cos(\alpha+\beta)=\frac{a^{2}-b^{2}}{a^{2}+b^{2}}.
Solution:
Step 1: Form a quadratic equation in terms of \cos~\theta
Given: a~\cos~\theta + b~\sin~\theta = c
b~\sin~\theta = c - a~\cos~\theta
Squaring both sides:
b^2~\sin^2~\theta = (c - a~\cos~\theta)^2
b^2(1 - \cos^2~\theta) = c^2 + a^2~\cos^2~\theta - 2ac~\cos~\theta
b^2 - b^2~\cos^2~\theta = c^2 + a^2~\cos^2~\theta - 2ac~\cos~\theta
(a^2 + b^2)\cos^2~\theta - 2ac~\cos~\theta + (c^2 - b^2) = 0
Since \alpha and \beta satisfy the original equation,
\cos~\alpha and \cos~\beta are the roots of this quadratic.
From the properties of quadratic roots:
Product~of~roots~(P_1) = \cos~\alpha~\cos~\beta = \frac{c^2 - b^2}{a^2 + b^2} …(i)
Step 2: Form a quadratic equation in terms of \sin~\theta
Start again with a~\cos~\theta + b~\sin~\theta = c.
a~\cos~\theta = c - b~\sin~\theta
Squaring both sides:
a^2~\cos^2~\theta = (c - b~\sin~\theta)^2
a^2(1 - \sin^2~\theta) = c^2 + b^2~\sin^2~\theta - 2bc~\sin~\theta
Bring all terms to one side:
(a^2 + b^2)\sin^2~\theta - 2bc~\sin~\theta + (c^2 - a^2) = 0
Here, \sin~\alpha and \sin~\beta are the roots.
Product~of~roots~(P_2) = \sin~\alpha~\sin~\beta = \frac{c^2 - a^2}{a^2 + b^2} …(ii)
Step 3: Calculate \cos(\alpha + \beta)
Recall the formula: \cos(\alpha + \beta) = \cos~\alpha~\cos~\beta - \sin~\alpha~\sin~\beta
Substitute values from (i) and (ii):
\cos(\alpha + \beta) = \frac{c^2 - b^2}{a^2 + b^2} - \frac{c^2 - a^2}{a^2 + b^2}
\cos(\alpha + \beta) = \frac{c^2 - b^2 - c^2 + a^2}{a^2 + b^2}
cos(\alpha + \beta) = \frac{a^2 - b^2}{a^2 + b^2}
Hence Proved.
Q33: How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid solution?
Solution:
Step 1: Define the variable and quantities
Let x be the litres of water added.
Existing solution volume = 1125 Litres.
Existing acid concentration = 45%.
Amount of pure acid = 45% \text{ of } 1125 = 0.45 \times 1125 = 506.25 Litres.
Water has 0% acid.
Step 2: Formulate the inequality
Total Volume of mixture = 1125 + x.
Total Acid in mixture = 506.25 (since water adds no acid).
We need the concentration (\frac{\text{Total Acid}}{\text{Total Volume}} \times 100) to be between 25% and 30%.
25 < \frac{506.25}{1125 + x} \times 100 < 30
Step 3: Solve the first part of the inequality (More than 25%)
25 < \frac{50625}{1125 + x}
25(1125 + x) < 50625
28125 + 25x < 50625
25x < 50625 - 28125
25x < 22500
x < \frac{22500}{25}
x < 900
Step 4: Solve the second part of the inequality (Less than 30%)
\frac{50625}{1125 + x} < 30
50625 < 30(1125 + x)
50625 < 33750 + 30x
50625 - 33750 < 30x
16875 < 30x
\frac{16875}{30} < x
562.5 < x
Final Answer: The amount of water to be added must be more than 562.5 litres and less than 900 litres.
Q34: Find the sum of the following series up to n terms: 5+55+555+5555...
Solution:
Step 1: Simplify the series
Let S_n = 5 + 55 + 555 + ... + \text{n terms}
Factor out 5:
S_n = 5 [1 + 11 + 111 + ... + \text{n terms}]
Multiply and divide by 9:
S_n = \frac{5}{9} [9 + 99 + 999 + ... + \text{n terms}]
Step 2: Express terms as powers of 10
We can write 9 as 10 - 1, 99 as 100 - 1, etc.
S_n = \frac{5}{9} [(10-1) + (10^2-1) + (10^3-1) + ... + (10^n-1)]
Step 3: Group the terms
Separate the powers of 10 and the -1s:
S_n = \frac{5}{9} [ (10 + 10^2 + ... + 10^n) - (1 + 1 + ... + 1) ]
Step 4: Apply GP formula
The first part is a Geometric Progression with a=10, r=10.
Sum of GP = a \frac{r^n - 1}{r - 1}
Sum = 10 \frac{10^n - 1}{10 - 1} = \frac{10}{9}(10^n - 1)
The second part is simply summing 1, n times, which equals n.
Step 5: Final Expression
S_n = \frac{5}{9} [ \frac{10}{9}(10^n - 1) - n ]
S_n = \frac{50}{81}(10^n - 1) - \frac{5n}{9}
Final Answer: \boxed{5 + 55 + 555 + ... + \text{n terms} = \frac{50}{81}(10^n - 1) - \frac{5n}{9}}
Q35: Find the derivative of f(x) using first principle where f(x) is
(a) \sin~x+\cos~x
(b) x~\sin~x
Solution
(a): f(x) = \sin~x + \cos~x
Step 1: Apply the definition of First Principle
f'(x) = \lim_{h\to 0} \frac{f(x+h) - f(x)}{h}
f'(x) = \lim_{h\to 0} \frac{[\sin(x+h) + \cos(x+h)] - [\sin~x + \cos~x]}{h}
Step 2: Group sine and cosine terms
f'(x) = \lim_{h\to 0} \frac{[\sin(x+h) - \sin~x] + [\cos(x+h) - \cos~x]}{h}
Step 3: Use Sum-to-Product formulas
\sin~A - \sin~B = 2\cos\frac{A+B}{2}\sin\frac{A-B}{2}
\cos~A - \cos~B = -2\sin\frac{A+B}{2}\sin\frac{A-B}{2}
Substituting A=x+h and B=x:
\sin(x+h) - \sin~x = 2\cos(x + \frac{h}{2})\sin(\frac{h}{2})
\cos(x+h) - \cos~x = -2\sin(x + \frac{h}{2})\sin(\frac{h}{2})
f'(x) = \lim_{h\to 0} \frac{2\cos(x + h/2)\sin(h/2) - 2\sin(x + h/2)\sin(h/2)}{h}
Step 4: Evaluate the limit
Factor out \sin(h/2):
f'(x) = \lim_{h\to 0} \frac{\sin(h/2)}{h/2} \cdot \frac{2}{2} [\cos(x+h/2) - \sin(x+h/2)]
Using \lim_{\theta\to 0} \frac{\sin~\theta}{\theta} = 1:
f'(x) = 1 \cdot [\cos(x+0) - \sin(x+0)]
f'(x) = \cos~x - \sin~x
(b): f(x) = x~\sin~x
Solution
Step 1: Apply definition
f'(x) = \lim_{h\to 0} \frac{(x+h)\sin(x+h) - x~\sin~x}{h}
f'(x) = \lim_{h\to 0} \frac{x~\sin(x+h) + h~\sin(x+h) - x~\sin~x}{h}
Step 2: Separate terms
f'(x) = \lim_{h\to 0} \left[ \frac{x(\sin(x+h) - \sin~x)}{h} + \frac{h~\sin(x+h)}{h} \right]
Step 3: Solve limits
First part: x \lim_{h\to 0} \frac{\sin(x+h) - \sin~x}{h}.
From part (a), we know this limit is the derivative of \sin~x, which is \cos~x.
Second part: \lim_{h\to 0} \sin(x+h) = \sin~x.
Step 4: Combine
f'(x) = x(\cos~x) + \sin~x
Final Answer: \boxed{ f'(x) = x(\cos~x) + \sin~x }
Q36: Find the mean deviation about the median for the data.
Solution:
Step 1: Construct the Frequency Distribution Table
| Income (Class) | Frequency f_i | Cumulative Frequency c.f. | Class Mark x_i | |x_i - M| | f_i|x_i - M| |
| 0-100 | 4 | 4 | 50 | 290 | 1160 |
| 100-200 | 8 | 12 | 150 | 190 | 1520 |
| 200-300 | 9 | 21 | 250 | 90 | 810 |
| 300-400 | 10 | 31 | 350 | 10 | 100 |
| 400-500 | 7 | 38 | 450 | 110 | 770 |
| 500-600 | 5 | 43 | 550 | 210 | 1050 |
| 600-700 | 4 | 47 | 650 | 310 | 1240 |
| 700-800 | 3 | 50 | 750 | 410 | 1230 |
| Total | N = 50 | Sum = 7880 |
Step 2: Find the Median ($M$)
N = 50 , so N/2 = 25.
The cumulative frequency just greater than 25 is 31.
Median Class: 300-400.
L = 300 (Lower limit), f = 10 (Frequency), cf = 21 (Preceding Cumulative Freq), h = 100 (Class width).
Median = L + \frac{\frac{N}{2} - cf}{f} \times h
M = 300 + \frac{25 - 21}{10} \times 100
M = 300 + \frac{4}{10} \times 100
M = 300 + 40 = 340
Step 3: Calculate Mean Deviation
Formula: M.D.(M) = \frac{\sum f_i |x_i - M|}{N}
Using the sum from the table:
M.D.(M) = \frac{7880}{50}
M.D.(M) = 157.6
Final Answer: Mean Deviation about Median is 157.6.
Section E – Case Study (4 marks each 1+1+2)
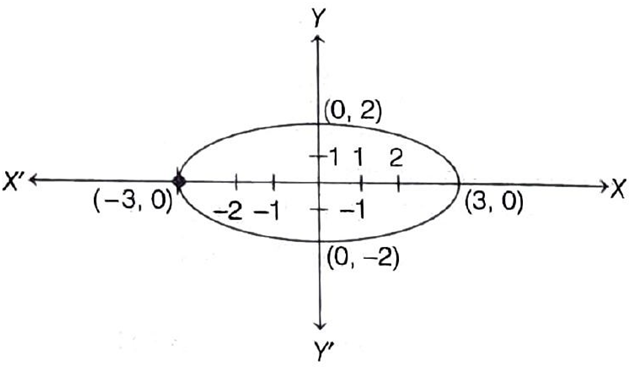
Q37: Due to a heavy storm, an electric wire got bent as shown in the figure (an ellipse). It followed a mathematical shape.
Answer the following question below.
- What is the equation of the shape of the curve?
- What is the eccentricity of the curve?
- What is the length of latus rectum for the curve?
i. What is the equation of the shape of the curve? From the figure provided in the question paper:
Solution:
The curve is an Ellipse with the major axis along the X-axis.
The vertices on the x-axis are (\pm 3, 0), so a = 3.
The vertices on the y-axis are (0, \pm 2), so b = 2.
The standard equation of an ellipse is:
\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1
Substitute a=3 and b=2:
\frac{x^2}{3^2} + \frac{y^2}{2^2} = 1
Final Answer: \boxed{ \frac{x^2}{9} + \frac{y^2}{4} = 1}
ii. What is the eccentricity of the curve?
The formula for eccentricity (e) when a > b is:
e = \sqrt{1 - \frac{b^2}{a^2}}
Substitute the values:
e = \sqrt{1 - \frac{4}{9}}
e = \sqrt{\frac{9-4}{9}}
e = \sqrt{\frac{5}{9}}
e = \frac{\sqrt{5}}{3}
Final Answer: \boxed{ e = \frac{\sqrt{5}}{3}}
iii. What is the length of latus rectum for the curve?
The formula for the length of the latus rectum (L) is:
L = \frac{2b^2}{a}
Substitute the values:
L = \frac{2(2)^2}{3}
L = \frac{2(4)}{3}
L = \frac{8}{3}
Final Answer: \boxed{ L = \frac{8}{3} } units
Q38: In a class of 60 students, 30 opted for NCC, 32 opted for NSS, and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that:
- The student has opted only NCC.
- The student opted for NCC and NSS.
- The student opted for neither NCC nor NSS
Solution:
Given Data:
Total Students n(S) = 60
NCC Cadets n(A) = 30
NSS Volunteers n(B) = 32
Both NCC and NSS n(A \cap B) = 24
i. The student has opted only NCC.
Number of students who opted for “Only NCC” is n(A) - n(A \cap B).
= 30 -24 = 6
Probability
P(\text{Only NCC}) = \frac{6}{60}
P(\text{Only NCC}) = \frac{1}{10}
Final Answer: \boxed{ P(\text{Only NCC}) = \frac{1}{10}}
ii. The student opted for NCC and NSS.
This refers to the intersection (students who took both).
The number is already given as 24.
Probability
P(A \cap B) = \frac{24}{60}
P(A \cap B) = \frac{2}{5}
Final Answer: \boxed{ \frac{2}{5}}
iii. The student opted for neither NCC nor NSS.
First, find the number of students who opted for at least one (Union).
n(A \cup B) = n(A) + n(B) - n(A \cap B)
n(A \cup B) = 30 + 32 - 24
n(A \cup B) = 38
Now, find those who opted for neither:
n(\text{Neither}) = \text{Total} - n(A \cup B)
n(\text{Neither}) = 60 - 38 = 22
Probability
P(\text{Neither}) = \frac{22}{60}
P(\text{Neither}) = \frac{11}{30}
Final Answer: \boxed{ \frac{11}{30}}