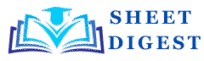Circle

A circle is a geometric shape that consists of all points in a plane that are equidistant from a fixed point called the center. The distance from the center to any point on the circle is called the radius. The line segment connecting the center to a point on the circle is also considered a radius.

Here are key features and properties of a circle:

1. Center: The fixed point in the plane from which all points on the circle are equidistant.
2. Radius: The distance from the center to any point on the circle. All radii of a circle are of equal length.
3. Diameter: A line segment passing through the center and connecting two points on the circle. The diameter is twice the length of the radius.
4. Circumference: The perimeter or boundary of the circle. The circumference is calculated using the formula C=2πr, where r is the radius.
5. Area: The region enclosed by the circle. The area is calculated using the formula A=πr^2, where r is the radius.
6. Chord: A line segment connecting two points on the circle.
7. Secant: A line that intersects the circle at two points.
8. Tangent: A line that touches the circle at exactly one point.

A circle is a two-dimensional shape and is often encountered in geometry and various mathematical applications. It has a symmetry property, meaning that any line passing through the center divides the circle into two equal halves.

Circles are essential in geometry, trigonometry, and calculus. They also appear in real-world applications, such as in the design of wheels, pulleys, orbits of celestial bodies, and more. Understanding the properties of circles is foundational in geometry and has broad applications in many areas of mathematics and science.

Equation of a circle

The general equation of a circle in a coordinate system with a center at (h,k) and a radius r is given by:
(x - h)^2 + (y - k)^2 = r^2

Here:

• (h,k) are the coordinates of the center of the circle.
• r is the radius of the circle.

This form can be useful when working with specific coordinates for the center.

For example, if the circle has a center at (3,−2) and a radius of 5, the equation would be:
(x - 3)^2 + (y +2 )^2 = 5^2
On simplifying we get: x^2+y^2-6x+4y-12=0

General Form of the Equation of a Circle

x^2+y^2+2gx+2fy+c=0

Here

• 𝑥 and 𝑦 are arbitrary points on the circumference of the circle
• 𝑔, 𝑓, and 𝑐 are constants

This general form is used to find the coordinates of the center of the circle and the radius.

• The center of the circle is (−𝑔,−𝑓)
• The radius is \sqrt{g^2+f^2-c}

Intercepts made by a circle on X Axis and Y Axis

Length of Intercept made by a circle on X axis: 2\sqrt{g^2-c}

Length of Intercept made by a circle on Y axis: 2\sqrt{f^2-c}