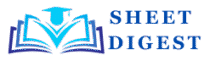Q1: Find the area under the given curves and given lines:
(i) y=x^{2}, x=1, x=2 and x-axis
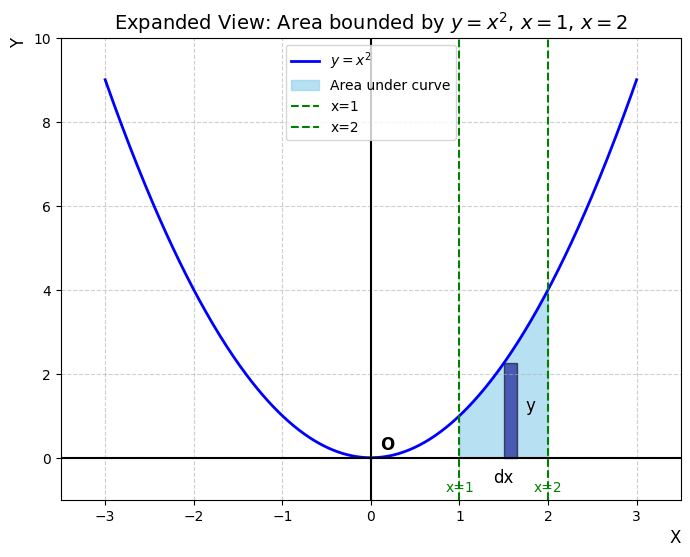
(ii) y=x^{4}, x=1, x=5 and x-axis
The formula is straightforward:
Area = \int_{a}^{b} y , dx. Since
Solution
Both curves y=x^2 and y=x^4 are standard parabolas opening upwards and lie above the x-axis for positive x, we don’t need to worry about absolute values or negative areas here.
(i) Step 1: Set up the Definite Integral
Formula for Area: Area = \int_{a}^{b} y , dx.
Since We need the area bounded by y=x^2 from x=1 to x=2.
A = \int_{1}^{2} x^2 , dx.
Step 2: Integrate
A = \left[ \frac{x^3}{3} \right]_{1}^{2}.
Step 3: Apply Limits Substitute the upper and lower limits:
A = \frac{1}{3} (8 - 1) A = \frac{7}{3}.
Final Answer (i): \boxed { \text{The area is: } \frac{7}{3} \text{ sq. units} }
(ii) Step 1: Set up the Definite Integral
Area bounded by y=x^4 from x=1 to x=5.
A = \int_{1}^{5} x^4 , dx.
Step 2: Integrate
A = \left[ \frac{x^5}{5} \right]_{1}^{5}.
Step 3: Apply Limits Substitute the limits:
A = \frac{1}{5} (3125 - 1) A = \frac{3124}{5} = 624.8.
Final Answer (ii): \boxed { \text{The area is: } 624.8 \text{ sq. units} }
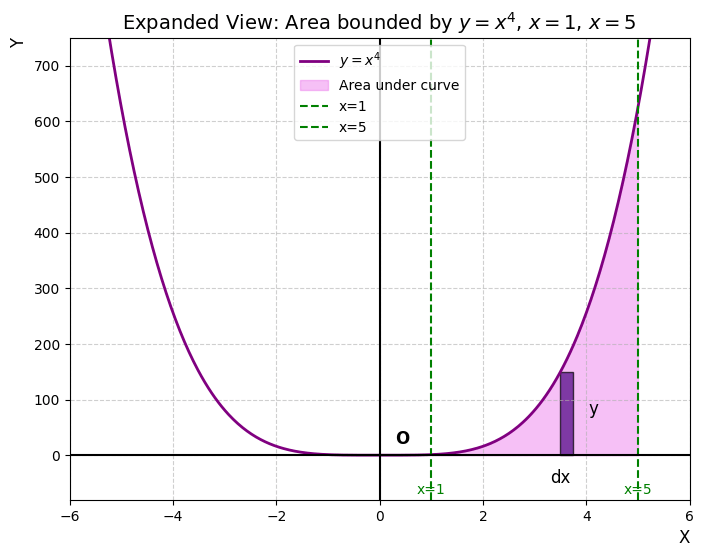
Q2: Sketch the graph of y=|x+3| and evaluate \int_{-6}^{0}|x+3|dx.
Solution:
To evaluate the integral from -6 to 0, we must break the integral at the critical point x = -3.
Step 1: Understand the Function and Sketch the Graph The function is defined as:
- Graph Description: The graph consists of two rays meeting at the vertex (-3, 0).
- To the left of x=-3, it is the line y = -x - 3 (slope -1).
- To the right of x=-3, it is the line y = x + 3 (slope +1).
- At the limits x=-6, y=|-6+3|=3.
- At the limit x=0, y=|0+3|=3.
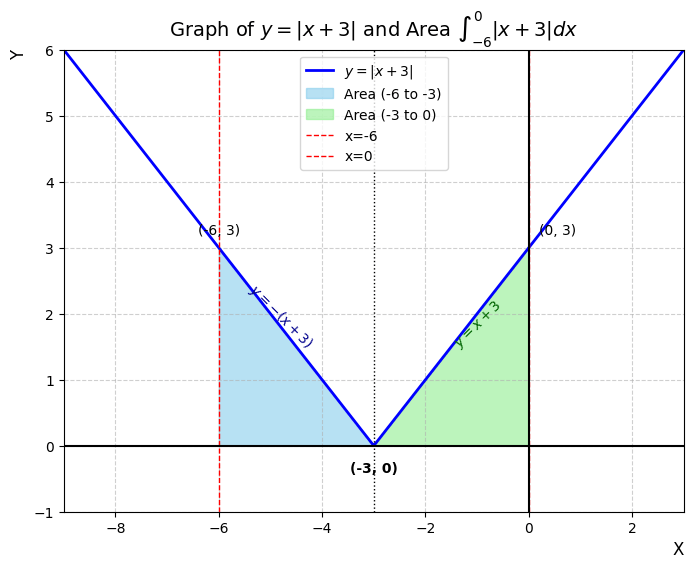
Step 2: Split the Definite Integral We split the integral limits at x=-3:
I = \int_{-6}^{0} |x+3| , dx = \int_{-6}^{-3} -(x+3) , dx + \int_{-3}^{0} (x+3) , dx.
Step 3: Integrate Each Part
Part 1 (Left side):
I_1 = - \left[ \left(\frac{(-3)^2}{2} + 3(-3)\right) - \left(\frac{(-6)^2}{2} + 3(-6)\right) \right]
I_1 = - \left[ -\frac{9}{2} - (18 - 18) \right]
I_1 = - \left[ -\frac{9}{2} - 0 \right] = \frac{9}{2}.
Part 2 (Right side):
I_2 = \int_{-3}^{0} (x+3) , dx = \left[ \frac{x^2}{2} + 3x \right]_{-3}^{0}
I_2 = \left[ (0 + 0) - \left(\frac{(-3)^2}{2} + 3(-3)\right) \right]
I_2 = - \left(-\frac{9}{2}\right) = \frac{9}{2}.
Step 4: Sum the Areas
Total Integral I = I_1 + I_2
I = \frac{9}{2} + \frac{9}{2} = \frac{18}{2} = 9.
Final Answer: \boxed{ \int_{-6}^{3} |x+3| dx = 9 }
Q3: Find the area bounded by the curve y=\sin x between x=0 and x=2\pi.
Solution
Step 1: Analyze the Curve
The curve is y = \sin x.
In the interval [0, \pi], \sin x \geq 0 (Curve is above x-axis).
In the interval [\pi, 2\pi], \sin x \leq 0 (Curve is below x-axis).
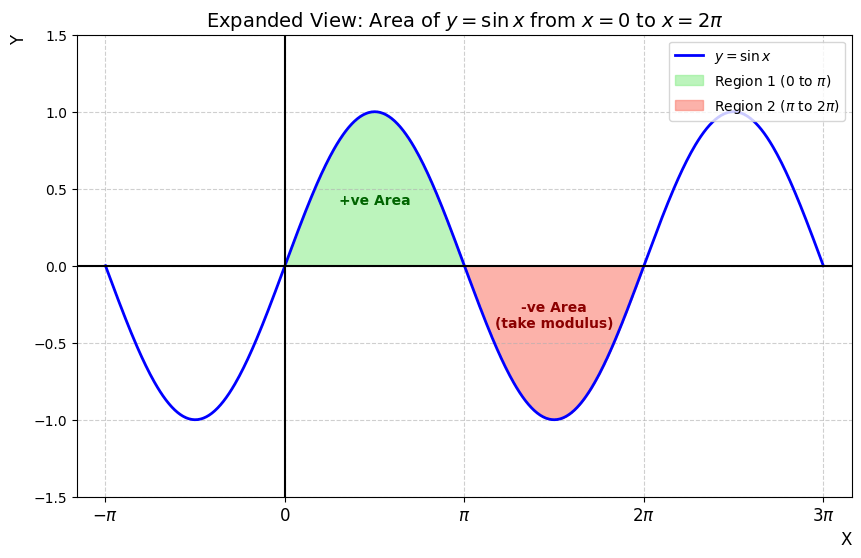
Therefore, the required area A is the sum of the areas of these two regions.
Step 2: Set up the Definite Integral
We split the limits at the x-intercept x = \pi:
A = \int_{0}^{\pi} \sin x , dx + \left| \int_{\pi}^{2\pi} \sin x , dx \right|
Step 3: Evaluate the First Part (0 to \pi)
A_1 = \left[ -\cos x \right]_{0}^{\pi}
A_1 = -(-1) - (-1) A_1 = 1 + 1 = 2.
Step 4: Evaluate the Second Part (\pi to 2\pi)
A_2 = \int_{\pi}^{2\pi} \sin x , dx
A_2 = \left[ -\cos x \right]_{\pi}^{2\pi}
A_2 = -(1) - (-(-1)) A_2 = -1 - 1 = -2.
To find the geometric area, we must treat the negative region as positive and take the absolute value of the second part
Since area cannot be negative, we take the absolute value: |A_2| = |-2| = 2.
Step 5: Calculate Total Area
A = 2 + 2 = 4.
Final Answer: \boxed {\text {The area bounded by the curve is: } 4 \text{ sq. units} }
Q4: Area bounded by the curve y=x^{3}, the x-axis and the ordinates x=-2 and x=1 is:
(A) -9
(B) \frac{-15}{4}
(C) \frac{15}{4}
(D) \frac{17}{4}
Teacher’s Insight: This is another excellent example of why sketching the graph is essential.
Solution:
Step 1: Plotting the Graph
Plotting the graph: The function y=x^3 is an odd function.
For x > 0, y is positive (graph is above the x-axis).
For x < 0, y is negative (graph is below the x-axis).

If we simply integrate from -2 to 1 directly, the negative area will subtract from the positive area, giving us an incorrect answer for the “geometric area”. We must split the integral at the origin x=0 and take the absolute value of the negative part.
Step 2: Split the Integral
The required area A is bounded by x=-2 and x=1.
The curve crosses the x-axis at x=0.
A = \left| \int_{-2}^{0} x^3 , dx \right| + \int_{0}^{1} x^3 , dx.
Step 2: Evaluate the First Part (Left of y-axis)
A_1 = \int_{-2}^{0} x^3 \ dx
A_1 = \left[ \frac{x^4}{4} \right]_{-2}^{0}
A_1 = \frac{0^4}{4} - \frac{(-2)^4}{4}
A_1 = 0 - \frac{16}{4} A_1 = -4.
Since area cannot be negative, we take the modulus: |A_1| = |-4| = 4.
Step 3: Evaluate the Second Part (Right of y-axis)
A_2 = \int_{0}^{1} x^3 \ dx
A_2 = \left[ \frac{x^4}{4} \right]_{0}^{1}
A_2 = \frac{1^4}{4} - 0 = \frac{1}{4}.
Step 4: Total Area
A = |A_1| + A_2
A = 4 + \frac{1}{4}
A = \frac{16}{4} + \frac{1}{4} = \frac{17}{4}.
Final Answer: The correct option is (D).
Q5: The area bounded by the curve y=x|x|, x-axis and the ordinates x=-1 and x=1 is given by:
(A) 0
(B) \frac{1}{3}
(C) \frac{2}{3}
(D) \frac{4}{3}
Solution:
Step 1: Plotting the curve:
We can simplify the function y = x|x|,by using the definition of absolute value:
If x \geq 0, then |x| = x, so y = x(x) = x^2 (an upward parabola).
If x < 0, then |x| = -x, so y = x(-x) = -x^2 (a downward parabola).
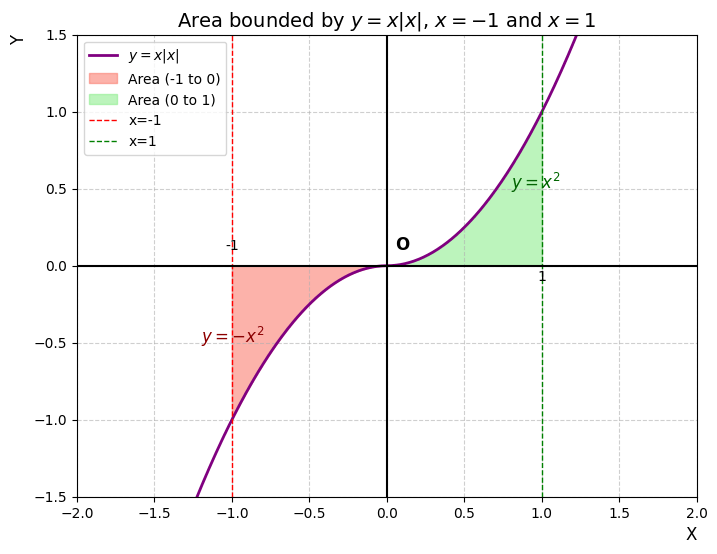
We must split the integral at x=0 because the curve flips from being below the axis to above it.
Step 2: Set up the Integrals
A = \text{Area left} + \text{Area Right}
A = \left| \int_{-1}^{0} x|x| , dx \right| + \int_{0}^{1} x|x| , dx.
Substituting the definitions of y: A = \left| \int_{-1}^{0} -x^2 \ dx \right| + \int_{0}^{1} x^2 \ dx.
Step 2: Evaluate the Left Area (x < 0)
I_1 = \int_{-1}^{0} -x^2 \ dx
I_1 = -\left[ \frac{x^3}{3} \right]_{-1}^{0}
I_1 = - \left( \frac{0}{3} - \frac{(-1)^3}{3} \right)
I_1 = - \left( 0 - \frac{-1}{3} \right) = - \frac{1}{3}.
Taking the absolute value for area: |I_1| = \frac{1}{3}.
Step 3: Evaluate the Right Area (x > 0)
I_2 = \int_{0}^{1} x^2 \ dx
I_2 = \left[ \frac{x^3}{3} \right]_ {0}^{1}
I_2 = \frac{1}{3} - 0 = \frac{1}{3}.
Step 4: Total Calculation A = \frac{1}{3} + \frac{1}{3} = \frac{2}{3}.
Final Answer: The Correct Option (C).