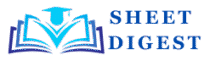Q 1: Find the area of the region bounded by the ellipse \frac{x^{2}}{16}+\frac{y^{2}}{9}=1.
Solution
Step 1: Identify the Curve and Coordinates
The given equation is an ellipse in the standard form \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. Comparing this with the given equation:
We find that:
a^2 = 16 \Rightarrow a = 4
b^2 = 9 \Rightarrow b = 3
Since a > b, the ellipse is horizontal (elongated along the x-axis).
The vertices on the x-axis are at x = -4 and x = 4.
Step 2: Use Symmetry to Simplify the Area
The ellipse is symmetrical about both the x-axis and the y-axis.
Therefore, the total area of the ellipse is 4 times the area of the region in the first quadrant (Area of region AOBA).
Total Area A = 4 \times \int_{0}^{a} y , dx.
Step 3: Express y in terms of x
We need the equation of the curve in the form y = f(x).
From the equation \frac{x^{2}}{16}+\frac{y^{2}}{9}=1:
\frac{y^{2}}{9} = 1 - \frac{x^{2}}{16}
\frac{y^{2}}{9} = \frac{16 - x^{2}}{16}
y^{2} = \frac{9}{16}(16 - x^{2})
Taking the square root
y = \pm \frac{3}{4}\sqrt{16 - x^{2}}.
(considering only the positive value since we are calculating the area in the first quadrant):
y = \frac{3}{4}\sqrt{16 - x^{2}}.
Step 4: Set up the Definite Integral
Now, substitute the value of y into our area formula:
A = 4 \int_{0}^{4} \frac{3}{4}\sqrt{16 - x^{2}} , dx
A = 3 \int_{0}^{4} \sqrt{4^2 - x^{2}} , dx.
Using the standard integration formula: \int \sqrt{a^2 - x^2} , dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right).
Here, a = 4.
Applying the limits from 0 to 4:
A = 3 \left[ \frac{x}{2}\sqrt{16 - x^2} + \frac{16}{2}\sin^{-1}\left(\frac{x}{4}\right) \right]_{0}^{4}
A = 3 \left[ \frac{x}{2}\sqrt{16 - x^2} + 8\sin^{-1}\left(\frac{x}{4}\right) \right]_{0}^{4}
Now, applying the upper and lower limits:
Upper limit (x = 4):
Lower limit (x = 0):
\left( \frac{0}{2}\sqrt{16 - 0} + 8\sin^{-1}(0) \right) = 0 + 0 = 0Final Calculation:
A = 3 [ 4\pi - 0 ]
A = 12\pi
Final Answer: \boxed { \text{The area of the region bounded by the ellipse is: } 12\pi \text{ sq. units} }
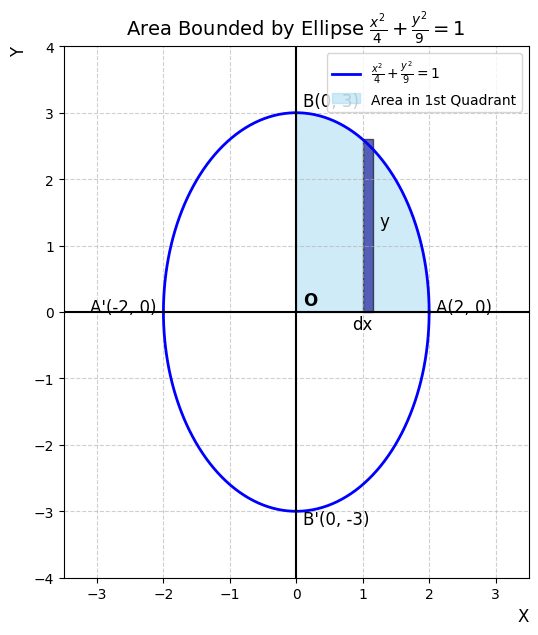
Q 2: Find the area of the region bounded by the ellipse \frac{x^{2}}{4}+\frac{y^{2}}{9}=1.
Teacher’s Insight: Similar to the first question, this is an ellipse centered at the origin. However, notice that the denominator of y^2 (which is 9) is larger than that of x^2 (which is 4). This tells us the ellipse is “tall” or vertical, stretching more along the y-axis.
Solution
Step 1: Identify the Curve and Coordinates The given equation is an ellipse in the form \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. Comparing this with the given equation:
We find that:
a^2 = 4 \Rightarrow a = 2
b^2 = 9 \Rightarrow b = 3
The vertices on the x-axis are at x = -2 and x = 2.
Step 2: Use Symmetry to Simplify the Area: The total area is 4 times the area of the region in the first quadrant.
Total Area A = 4 \times \int_{0}^{2} y , dx.
Step 3: Express y in terms of x
Using the equation \frac{x^{2}}{4}+\frac{y^{2}}{9}=1
\frac{y^{2}}{9} = 1 - \frac{x^{2}}{4}
\frac{y^{2}}{9} = \frac{4 - x^{2}}{4}
y^{2} = \frac{9}{4}(4 - x^{2})
Taking the square root
y = \pm \frac{3}{2}\sqrt{4 - x^{2}}
y = \frac{3}{2}\sqrt{4 - x^{2}}. (considering only the positive value for the first quadrant)
Step 4: Set up the Definite Integral Substitute y into the area formula:
A = 4 \int_{0}^{2} \frac{3}{2}\sqrt{4 - x^{2}} , dx
A = 4 \times \frac{3}{2} \int_{0}^{2} \sqrt{2^2 - x^{2}} , dx
A = 6 \int_{0}^{2} \sqrt{2^2 - x^{2}} , dx.
Using the formula: \int \sqrt{a^2 - x^2} , dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right).
Here, a = 2.
Applying limits from 0 to 2:
A = 6 \left[ \frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right) \right]_{0}^{2}
A = 6 \left[ \frac{x}{2}\sqrt{4 - x^2} + 2\sin^{-1}\left(\frac{x}{2}\right) \right]_{0}^{2}
Applying Upper limit (x = 2):
Applying Lower limit (x = 0):
\left( \frac{0}{2}\sqrt{4 - 0} + 2\sin^{-1}(0) \right) = 0 + 0 = 0Final Calculation:
A = 6\pi
Final Answer: \boxed { \text{The area of the region bounded by the ellipse is: } 6\pi \text{ sq. units} }
Q 3: Find the area lying in the first quadrant and bounded by the circle x^{2}+y^{2}=4 and the lines x=0 and x=2.
(A) \pi
(B) \frac{\pi}{2}
(C) \frac{\pi}{3}
(D) \frac{\pi}{4}
Solution
Step 1: Identify the Curve and Coordinates
The equation x^2 + y^2 = 4 represents a circle centered at the origin with radius r = 2
(since r^2 = 4).
The region is bounded by:
The curve y = \sqrt{4-x^2}
The lines x=0 (y-axis) and x=2.

Step 2: Set up the Definite Integral
We need the area in the first quadrant only:
Therefore, A = \int_{0}^{2} y , dx.
Step 3: Express y in terms of x From x^2 + y^2 = 4:
latex]y = \pm \sqrt{4 – x^2}[/latex]
y = \sqrt{4 - x^2} (Taking positive root for 1st quadrant).
Step 4: Evaluate the Integral
A = \int_{0}^{2} \sqrt{2^2 - x^2} , dx.
Using Formula \int \sqrt{a^2 - x^2} , dx = \frac{x}{2}\sqrt{a^2 - x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)
with a=2:
A = \left[ \frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\left(\frac{x}{2}\right) \right]_{0}^{2}
A = \left[ \frac{x}{2}\sqrt{4 - x^2} + 2\sin^{-1}\left(\frac{x}{2}\right) \right]_{0}^{2}
Applying Upper limit (x = 2):
Applying Lower limit (x = 0):
\left( 0 + 2\sin^{-1}(0) \right) = 0Final Calculation:
A = \pi - 0 = \piFinal Answer: Correct Option A
Q 4: Find the area of the region bounded by the curve y^{2}=4x, y-axis and the line y=3.
(A) 2
(B) \frac{9}{4}
(C) \frac{9}{3}
(D) \frac{9}{2}
Solution
When the boundary is the y-axis, it is much easier to integrate with respect to y (using horizontal strips) rather than x.
Formula for area bounded by the y-axis: A = \int_{c}^{d} x , dy.
Step 1: Identify the Curve and Coordinates
Curve: y^2 = 4x is a right-handed parabola with vertex at origin.
Boundaries: The y-axis (x=0) and the horizontal line y=3.
Limits of Integration: Since the region starts from the vertex (on the x-axis, where y=0) and goes up to y=3, our limits are y=0 to y=3.

Step 2: Express x in terms of y
Given y^2 = 4x
x = \frac{y^2}{4}
Step 3: Set up the Definite Integral
Using formula A = \int_{a}^{b} x , dy
A = \int_{0}^{3} \frac{y^2}{4} , dy
A = \frac{1}{4} \int_{0}^{3} y^2 , dy
A = \frac{1}{4} \left[ \frac{y^3}{3} \right]_{0}^{3}
A = \frac{1}{12} \left[ y^3 \right]_{0}^{3}
Applying Limits:
A = \frac{1}{12} (27)
A = \frac{27}{12}
A = \frac{9}{4}
Simplifying the fraction (dividing numerator and denominator by 3):
Final Answer: Correct option B