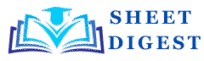Intoduction
Have you solved Class 10 CBSE Maths Practice Paper 2026 and are looking for a solutions to the questons? Here you’ll find complete, step-by-step NCERT-style solutions for every question. Designed for both students and teachers, these answers make board exam revision easier with clear explanations, formula highlights, and downloadable PDF options.
Class 10 Full Syllabus Practice Question Paper-1 2026 ⇒
Solution to the paper.
Section A — Multiple Choice Questions (1 mark each)
Q1. Given that HCF (48, a) = 3 and LCM (48, a) = 144. Find the value of a.
Options: (A) 6 (B) 8 (C) 9 (D) 12
Solution:
Use the relation:
\text{HCF} \times \text{LCM} = \text{Product of the two numbers}
48 \times a = 3 \times 144
48a = 432
a = \dfrac{432}{48} = 9
✅ Correct Option: (C)
Q2. Find the value of k if 12x^2 + kx + 27 = 0 has equal roots.
Options: (A) 30 (B) -36 (C) 39 (D) None of these
Solution:
12x^2 + kx + 27 = 0
a = 12 \ \ b = k \ \ c = 27
For equal roots, discriminant = 0.
\Delta = b^2 - 4ac = 0
k^2 - 4(12)(27) = 0
k^2 = 1296
k = \pm 36
✅ Correct Option: (B)
Q3. The mode of 7 observations is 17. The observations are 8, 2, 17, x, 17, 11, 2. Find x.
Options: (A) 2 (B) 8 (C) 10 (D) 17
Solution:
To make 17 the unique mode, it must appear the most times.
If x = 17, frequency of 17 becomes 3 — highest.
✅ Correct Option: (D)
Q4. If \cosec\theta - \cot\theta = m, find \cosec\theta + \cot\theta.
Options: (A) m (B) \dfrac{1}{m} (C) m^2 (D) 2m
Solution:
Use identity: \cosec^2\theta - \cot^2\theta = 1
(\cosec\theta + \cot\theta)(\cosec\theta - \cot\theta) = 1
Given: \cosec\theta - \cot\theta = m
Hence, (\cosec\theta + \cot\theta)m = 1
\cosec\theta + \cot\theta = \dfrac{1}{m}
✅ Correct option: (B)
Q5. Find the length of the tangent from a point 41 cm away from the centre of a circle of radius 9 cm.
Options: (A) 40 cm (B) 9 cm (C) 41 cm (D) 50 cm
Solution:
Radius OT = 9cm
Point from center OP = 41cm
Using Pythagoras theorem
Length of tangent PT = \sqrt{OP^2 - OT^2}
PT = \sqrt{41^2 - 9^2}
PT = \sqrt{1681 - 81}
PT = \sqrt{1600}
PT = 40
✅ Correct Option: (A)
Q6. Find the probability of selecting a consonant from the word “HYDERABAD”.
Options: (A) \dfrac{1}{3} (B) \dfrac{2}{3} (C) \dfrac{8}{9} (D) \dfrac{7}{9}
Solution:
Total letters = 9
Vowels = A, A, E = 3
Consonants = H, Y, D, R, B, D = 6
Probability of consonants = \dfrac{6}{9} = \dfrac{2}{3}
✅ Correct Option: (B)
Q7. If A(8, -4) and O(0, 0) are the ends of a diameter, find the centre.
Options: (A) (0, 0) (B) (16, -2) (C) (4, -2) (D) (-4, 2)
Solution:
Centre = midpoint of endpoints.
Centre = \left(\dfrac{8+0}{2}, \dfrac{-4+0}{2}\right)
Centre = (4, -2)
✅ Correct Option: (C)
Q8.A right triangle ABC, right-angled at A, circumscribes a circle of radius 5 cm. If AB = 18 cm and AC = 17 cm, find OC.
Options: (A) 10 cm (B) 9 cm (C) 12 cm (D) 13 cm
Solution:
Construction: Join OD from centre (O) to point of contact (D)
Since the radius meets the tangent at 90o
\therefore \angle ODA = \angle OEA = 90^{o}
Given \angle DAE = 90^{o}
Therefore ADOE is a square
\rightarrow OD = AD = 5cm
CD = CA - AD
CD = 17 - 5
CD = 12
In \triangle OCD
Using Pythagoras Theorem
OC^{2} = CD^{2} + OD^{2}
OC^{2} = 12^{2} + 5^{2}
OC^{2} = 144 + 25
OC^{2} = 169
OC = 13
✅ Correct Option: (D)
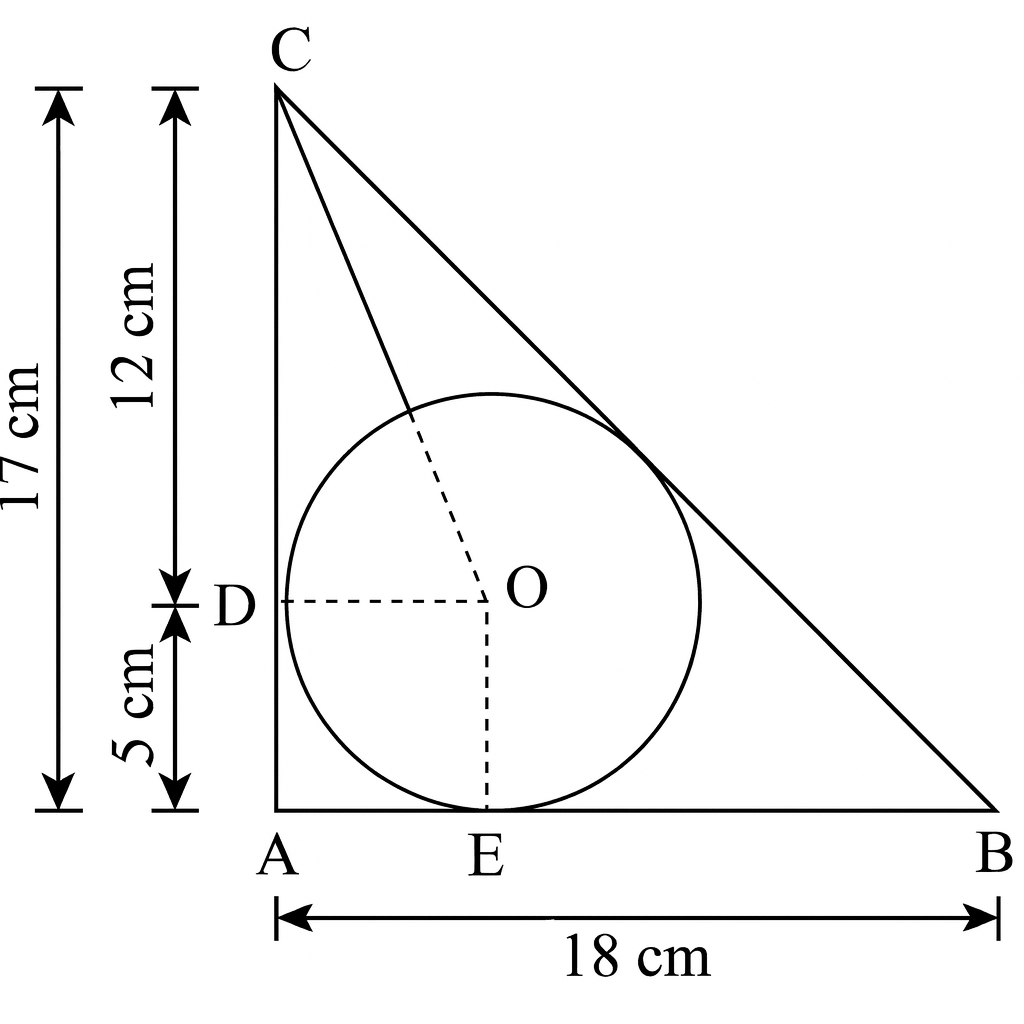
Q9. What type of polynomial f(x) is represented in the graph given below?
Options: (A) Linear (B) Quadratic (C) Cubic (D) Constant
Solution: Qudratic Polynomial
✅ Correct Option: (B)
Q10. The sum of 3 consecutive terms of an AP is 51. Find the middle term.
Options: (A) 17 (B) 16 (C) 19 (D) 18
Solution:
Let terms be (a - d), a, (a + d)
Given Sum = 51
(a-d) + a + (a+d) = 51
3a = 51
a = 17
✅ Correct Option: (A)
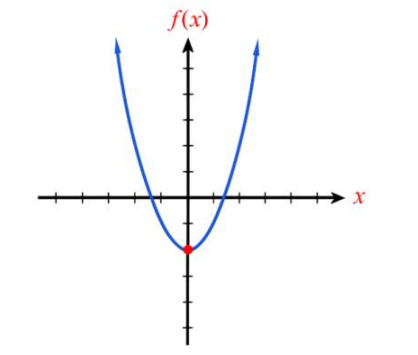
Q11. The angle of elevation of the top of a 55 m tower at a point 55 m away is
Options: (A) 30° (B) 40° (C) 45° (D) 60°
Solution:
Tower: AB
In \triangle ABP
\tan \theta = \dfrac{AB}{BP}
\tan \theta = \dfrac{55}{55}
\tan \theta = 1
\tan \theta = \tan 45^\circ
\theta = 45^\circ
✅ Correct Option: (C)
Q12. Heights of two cones are in ratio 1:3 and their radii are in ratio 3:1. Find the ratio of their volumes.
Options: (A) 1:1 (B) 1:3 (C) 3:1 (D) 3:3
Solution:
Let the heights be h \ and \ 3h
Let the radius be 3r \ and \ 3
Formula of volume
V = \pi r^{2} h
\frac{V_1}{V_2} = \frac{\pi (3r)^{2} h}{\pi r^{2} (3h)}
\frac{V_1}{V_2} = \frac{ 9r^{2} h}{ r^{2} (3h)}
\frac{V_1}{V_2} = \frac{3}{1)}
\frac{V_1}{V_2} = 3:1
✅ Correct Option: (C)
Q13. An urn contains 5 red, 6 blue and 8 yellow balls. Find the probability of selecting a red ball.
Options: (A) \frac{5}{8} (B) \frac{6}{8} (C) \frac{6}{19} (D) \frac{5}{19}
Solution:
Red Balls = 5
Blue Balls = 6
Yellow Balls = 8
Total balls = 5 + 6 + 8 = 19
Probability (red) = \dfrac{5}{19}
✅ Correct Option: (D)
Q14. A regular pentagon is inscribed in a circle with centre O, of radius 5 cm, as shown below.
What is the area of the shaded part of the circle?
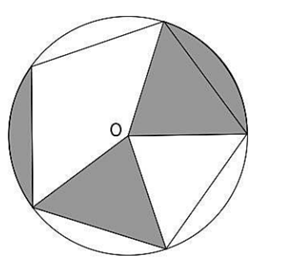
Options: (A) 2\pi (B) 4\pi (C) 5\pi (D) 10\pi
Solution:
Given Radius = 5cm
Each sector angle = \dfrac{360^\circ}{5} = 72^\circ
Area of shaded region = Area of 2 sectors
Area of shaded region = 2 X Area of 1 sector
Area of shaded region = 2 \times \dfrac{72}{360} \pi r^2
Area of shaded region = 2 \times \dfrac{1}{5} \pi (5)^2
Area of shaded region = 2 \times 5\pi
Area of shaded region = 10 \pi
✅ Correct Option: (D)
Q15. If x = a\cos\theta and y = b\sin\theta, find b^2x^2 + a^2y^2.
Options: (A) a^{2}b^{2} (B) ab (C) a^{4}b^{4} (D)a^{2} + b^{2}
Solution:
b^2x^2 + a^2y^2 = b^2a^2\cos^2\theta + a^2b^2\sin^2\theta
b^2x^2 + a^2y^2 = a^2b^2(\cos^2\theta + \sin^2\theta)
b^2x^2 + a^2y^2 = a^2b^2
✅ Correct Option: (A)
Q16. The probability of selecting a bad apple from 400 apples is 0.035. Find the number of bad apples.
Options: (A)7 (B) 14 (C) 21 (D) 28
Solution:
Using formula of probability
\text{probability of bad apples} = \frac{\text{Number of bad apples}}{\text{Total Number of apples}}
\text{Number of bad apples} = {\text{Total Number of apples}} \times \text{probability of bad apples}
\text{Number of bad apples} = 400 \times 0.035
\text{Number of bad apples} = 14
✅ Correct Option (B)
Q17. Two scalene triangles are given below.
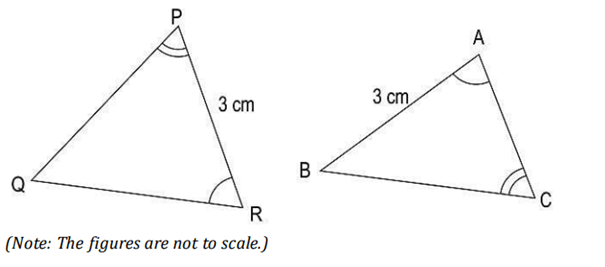
Anas and Rishi observed them and said the following:
Anas: ΔPQR is similar to ΔCBA.
Rishi: ΔPQR is congruent to ΔCBA.
Which of them is/are correct?
Options: (A) Only Anas (B) Only Rishi (C) Both Anas and Rishi
(D) Neither of them, as two scalene triangles can never be similar or congruent.
Solution:
Considering Anas’s statement
\angle A = \angle R
\angle C = \angle P
Therefore using AA criteria \triangle ABC \sim \triangle PQR
Hence, Anas’s statement is correct
Considering Rishi’s statement
Although 2 angles and a side of \triangle PQR are equal to 2 angles and side of \triangle ABC , the triangles cannot be proved congruent
Since In \triangle PQR the side PR is included between \angle P and \angle R
But In \triangle ABC the side AB is not included between \angle A and \angle C
✅ Correct Option: (A)
Q18. In \triangle OTA, tangent AT touches circle the radius and OT = 6\text{ cm} and \angle OTA = 45^\circ. Find AT.
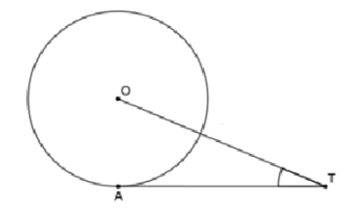
Options: (A) 3 \sqrt{2} (B) 3 (C) 3 \sqrt{3} (D) 4
Solution:
In \triangle OTA, Right right angled at T,
\cos T = \dfrac{AT}{OT}
\cos45^\circ = \dfrac{AT}{OT}
\frac{1}{\sqrt{2}} = \dfrac{AT}{6}
AT = \frac{6}{\sqrt{2}}
AT = 3\sqrt{2}
✅ Correct Option: (A)
Instructions for For questions 19 and 20
Two statements are given below – one labelled Assertion (A) and the other labelled Reason (R).
Read the statements carefully and choose the option that correctly describes statements (A) and (R).
Q19. Assertion (A): The origin is the only point equidistant from (2, 3) and (-2, -3).
Reason (R): The origin is the midpoint of the line joining them.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
Points equidistant lie on perpendicular bisector (many points). So (A) is false, (R) is true.
✅ Correct Option: (D)
Q20. Assertion (A): Two tangents drawn to a circle from an external point subtend equal angles at the centre.
Reason (R): A parallelogram circumscribing a circle is a rhombus.
(A) Both (A) and (R) are true and (R) is the correct explanation for (A).
(B) Both (A) and (R) are true but (R) is not the correct explanation for (A).
(C) (A) is true but (R) is false.
(D) (A) is false but (R) is true.
Solution:
Both statements true, but R doesn’t explain A.
✅ Correct Option (B)
Section B — Very Short Answer Type Questions (2 marks each)
Q21. Aman and David visited the same store on the 1st of January. If Aman visits the store every 4th day and David visits the store every 7th day, on which date will they visit the store together again?
Solution:
Step 1. Frequency of Aman’s visits = 4\ \text{days}
Frequency of David’s visits = 7\ \text{days}
Step 2. They will visit together again after the LCM of 4 and 7 days.
\text{LCM}(4,7)=28\ \text{days}
Step 3. They first met on 1st January, so their next common visit will be after 28 days.
Step 4. Counting 28 days from 1st January: 1 + 28 = 29.
Final Answer: \boxed{\text{They will visit the store together again on 29th January.}}
Q22. Evaluate 3\sin30^\circ-1+2\cos^{2}45^\circ-4\sin^{2}30^\circ
Solution:
Step 1. Write known values.
\sin30^\circ=\dfrac{1}{2}
\cos45^\circ=\dfrac{\sqrt{2}}{2}
Step 2. Substitute and simplify termwise.
3\sin30^\circ=3\cdot\dfrac{1}{2}=\dfrac{3}{2}
2\cos^{2}45^\circ=2\left(\dfrac{\sqrt{2}}{2}\right)^{2}=2\cdot\dfrac{1}{2}=1
4\sin^{2}30^\circ=4\left(\dfrac{1}{2}\right)^{2}=4\cdot\dfrac{1}{4}=1
Step 3. Combine all terms.
3\sin30^\circ-1+2\cos^{2}45^\circ-4\sin^{2}30^\circ=\dfrac{3}{2}-1+1-1
3\sin30^\circ-1+2\cos^{2}45^\circ-4\sin^{2}30^\circ=\dfrac{1}{2}
Final answer: \boxed{3\sin30^\circ-1+2\cos^{2}45^\circ-4\sin^{2}30^\circ = \dfrac{1}{2}}
Q23. Solve the pair of linear equations 12x + 8y = 56 and 8x + 12y = 44
Solution:
Step 1. Write both equations.
12x + 8y = 56 \quad ...(1)
8x + 12y = 44 \quad …(2)
Step 2. Multiply to eliminate one variable (make coefficients of y equal).
Multiply (1) by 3 and (2) by 2:
36x + 24y = 168 \quad ...(3)
16x + 24y = 88 \quad …(4)
Step 3. Subtract (4) from (3).
(36x - 16x) + (24y - 24y) = 168 - 88
20x = 80
x = 4
Step 4. Substitute x = 4 in (1).
12(4) + 8y = 56
48 + 8y = 56
8y = 8
y = 1
Final Answer: \boxed{x = 4,\ y = 1}
Q24. Two parallel tangents are drawn to a circle whose area is 25\pi\ \text{cm}^2. Find the distance between the points of contact.
Solution:
Given: Area = 25\pi\ \text{cm}^2
Step 1. Write in terms of formula for the area of a circle.
\pi r^2 = 25\pi
Step 2. Solve for radius.
r^2 = 25
r = 5\text{ cm}
Step 3. Distance between two parallel tangents to a circle = 2r.
2r = 2(5) = 10\text{ cm}
Final Answer: \boxed{\text{Distance between tangents} = 10\text{ cm}}
Q25. Two dice are rolled together. Find the probability that the sum of the numbers obtained is less than 5.
Solution:Step 1. Write the possible sums when two dice are rolled.
Possible sums = 2,3,4,5,6,7,8,9,10,11,12
Step 2. Count outcomes where sum < 5.
Sum = 2 → (1,1) → 1 way
Sum = 3 → (1,2), (2,1) → 2 ways
Sum = 4 → (1,3), (2,2), (3,1) → 3 ways
Total favourable outcomes = 1 + 2 + 3 = 6.
Step 3. Total possible outcomes when two dice are rolled = 6 \times 6 = 36.
Step 4. Probability = \dfrac{\text{Favourable outcomes}}{\text{Total Possible outcomes}} = \dfrac{6}{36} = \dfrac{1}{6}
Final Answer: \boxed{P(\text{sum} < 5) = \dfrac{1}{6}}
Section C — Short Answer Type Questions (3 marks each)
Q26. Find the zeroes of the polynomial x^{2}-5 and verify the relationship between zeroes and coefficients of the polynomial.
Solution:
Step 1. Solve x^{2}-5=0.
x^{2}=5
x=\pm\sqrt{5}
\therefore \quad \alpha=\sqrt{5},\ \beta=-\sqrt{5}.
Step 2. Sum and product of zeroes from roots.
Let zeroes be \alpha=\sqrt{5},\ \beta=-\sqrt{5}.
\alpha+\beta=\sqrt{5}-\sqrt{5}=0
\alpha\beta=(\sqrt{5})(-\sqrt{5})=-5
Step 3. Identify coefficients of x^{2}+0\cdot x-5.
latex]a=1,\quad b=0,\quad c=-5[/latex]
Step 4. Verify relations with coefficients.
Sum of zeroes should equal -\dfrac{b}{a}=-\dfrac{0}{1}=0. Verified.
Product of zeroes should equal \dfrac{c}{a}=\dfrac{-5}{1}=-5. Verified.
Final answer: \boxed{\text{Zeroes }=\pm\sqrt{5};\ \alpha+\beta=0=-\dfrac{b}{a},\ \alpha\beta=-5=\dfrac{c}{a}} \ \text{Relationship Verified}
Q27. Prove that \sqrt{7} is irrational.
Solution:
Step 1. Assume contrary that \sqrt{7} is rational.
Then there exist coprime integers p,q with q\ne0 such that
\sqrt{7}=\dfrac{p}{q}
Step 2. Square both sides.
7=\dfrac{p^{2}}{q^{2}}
\Rightarrow 7q^{2}=p^{2} … (1)
Step 3. Conclude divisibility by 7.
From 7q^{2}=p^{2} we get 7 \text{is a factor of } p^{2}
\Rightarrow 7 \text{is also a factor of } p. By Theorem
So write p=7k for some integer k.
Step 4. Substitute back in (1).
7q^{2} = (7k)^{2}
7q^{2} = 49k^{2}
\Rightarrow q^{2}=7k^{2}
Hence 7 \text{ is a factor of } q^{2}
\Rightarrow 7\text {is also a factor of } q. By Theorem
Step 5. Contradiction.
Both p and q are divisible by 7 contradicting that they are coprime.
This contradiction arises because of our wrong assumption that \sqrt{7} is rational.
Hence Proved: \boxed{\sqrt{7}\text{ is irrational}}
Q28. Prove that \dfrac{\sin^{2}\theta}{\cos^{2}\theta}+\dfrac{\cos^{2}\theta}{\sin^{2}\theta}=\dfrac{1}{\sin^{2}\theta\cos^{2}\theta}-2
Solution:
Step 1. Write left side as sum of squares.
LHS = \dfrac{\sin^{2}\theta}{\cos^{2}\theta}+\dfrac{\cos^{2}\theta}{\sin^{2}\theta}
LHS =\tan^{2}\theta+\cot^{2}\theta
Step 2. Convert to common denominator.
LHS = \dfrac{\sin^{4}\theta+\cos^{4}\theta}{\sin^{2}\theta\cos^{2}\theta}
Step 3. Simplify numerator using identity
\sin^{4}\theta+\cos^{4}\theta=(\sin^{2}\theta+\cos^{2}\theta)^{2}-2\sin^{2}\theta\cos^{2}\theta.
Since we know \sin^{2}\theta+\cos^{2}\theta=1,
Therefore \sin^{4}\theta+\cos^{4}\theta=1-2\sin^{2}\theta\cos^{2}\theta
Step 4. Substitute into fraction.
LHS = \dfrac{1-2\sin^{2}\theta\cos^{2}\theta}{\sin^{2}\theta\cos^{2}\theta}
LHS =\dfrac{1}{\sin^{2}\theta\cos^{2}\theta}-2
LHS = RHS
Hence Proved: \boxed{\dfrac{\sin^{2}\theta}{\cos^{2}\theta}+\dfrac{\cos^{2}\theta}{\sin^{2}\theta}=\dfrac{1}{\sin^{2}\theta\cos^{2}\theta}-2}
Q29. (A) The area of a rectangle reduces by 160\ \text{m}^2 if its length is increased by 5\ \text{m} and breadth reduced by 4\ \text{m}. However, if the length is decreased by 10\ \text{m} and breadth increased by 2\ \text{m}, its area is decreased by 100\ \text{m}^2. Find the dimensions of the rectangle.
Solution:
Step 1. Let original length = l and breadth = b. Original area = A=lb.
Step 2. Translate first condition.
(l+5)(b-4)=lb-160
lb+5b-4l-20=lb-160
5b-4l-20=-160
5b-4l=-140
4l-5b=140\quad ...(1)
Step 3. Translate second condition.
(l-10)(b+2)=lb-100
lb-10b+2l-20=lb-100
-10b+2l-20=-100
2l-10b=-80
Divide by 2:
l-5b=-40\quad ...(2)
Step 4. Solve (1) and (2). Subtract (2) from (1):
From (1): 4l-5b=140
From (2): l-5b=-40
Subtract:
3l=140-(-40)
3l=180
l=60
Step 5. Find breadth. Use (2):
60-5b=-40
-5b=-100
b=20
Final answer: \boxed{\text{Length}=60\ \text{m},\ \text{Breadth}=20\ \text{m}}
Q29. (B) If 16 is subtracted from twice the greater of two positive numbers, the result is half the other number. If 1 is subtracted from half the greater number, the result is still half the other number. Find the two numbers.
Solution:
Step 1. Let greater number = x and the other number = y (both positive).
2x-16=\dfrac{y}{2} \quad ...(1)
\dfrac{x}{2}-1=\dfrac{y}{2} \quad …(2)
Step 2. Equate (1) and (2) (both equal \dfrac{y}{2}).
2x-16=\dfrac{x}{2}-1
Step 3. Multiply by 2 and solve for x.
4x-32=x-2
3x=30\Rightarrow x=10
Step 4. Find y using (2).
\dfrac{10}{2}-1=\dfrac{y}{2}\Rightarrow 5-1=\dfrac{y}{2}\Rightarrow \dfrac{y}{2}=4
y=8
Final answer: \boxed{\text{The two numbers are }10\text{ and }8}
Q30. A circus tent is a cylinder surmounted by a cone of the same diameter. Common diameter = 56\ \text{cm}. Height of cylindrical part = 6\ \text{m}. Total height = 27\ \text{m}. Find the area of canvas used. (Give answer in \text{m}^2. Take \pi=\dfrac{22}{7}.)
Solution:
Step 1. Radius and heights.
r=\dfrac{56}{2}=28\ \text{m}
h_{\text{cyl}}=6\ \text{m}
h_{\text{cone}}=27-6=21\ \text{m}
Step 2. Slant height of cone.
l=\sqrt{r^{2}+h_{\text{cone}}^{2}}=\sqrt{28^{2}+21^{2}}=\sqrt{784+441}=\sqrt{1225}=35\ \text{m}
Step 3. Curved surface areas.
Cylinder CSA
\text{CSA}_{\text{cyl}}=2\pi r h=2\pi\cdot 28\cdot 6=336\pi
Cone CSA:
\text{CSA}_{\text{cone}}=\pi r l=\pi\cdot 28\cdot 35=980\pi
Step 4. Total canvas area.
\text{Total}=336\pi+980\pi=1316\pi
Step 5. Substitute \pi=\dfrac{22}{7} and simplify.
\text{Total}=1316\cdot\dfrac{22}{7}=\dfrac{1316}{7}\cdot 22=188\cdot 22=4136
Final answer: \boxed{\text{Canvas area used}=4136\ \text{m}^2}
Q31. In triangle ABC the sides AB, BC and CA touch a circle with centre O and radius r at P, Q and R respectively.
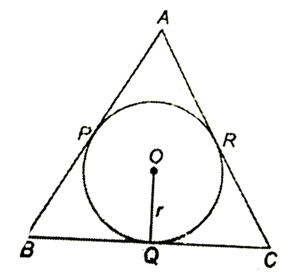
Prove that:
(i) AB + CQ = AC + BQ
(ii) \text{Area }(\triangle ABC)=\dfrac{1}{2}\times\text{Perimeter}(\triangle ABC)\times r
Solution:
Step 1. Use tangent-length property. Tangents drawn from the same external point to a circle are equal:
AP=AR,\quad BP=BQ,\quad CQ=CR.
(i) Express AB, AC in terms of tangent segments.
AB=AP+BP
AC=AR+CR
Compute AB+CQ:
AB+CQ=(AP+BP)+CQ
Using equalities: AP=AR,\ CQ=CR so
AB+CQ=(AR+BP)+CR
AB+CQ=AR+CR+BP
AB+CQ=AC+BP
since BP=BQ.
AB+CQ=AC+BQ
Hence proved \boxed{\text{(i) }AB+CQ=AC+BQ}
(ii) Area via three right triangles with height r.
Area of \triangle ABC = sum of areas of triangles with bases equal to sides and common altitude r from points of contact to each side:
\text{Area}=\dfrac{1}{2}(AB\cdot r)+\dfrac{1}{2}(BC\cdot r)+\dfrac{1}{2}(CA\cdot r)
\text{Area}= \dfrac{1}{2}r(AB+BC+CA)
But AB+BC+CA is the perimeter P. Therefore
\text{Area}=\dfrac{1}{2} \cdot P \cdot r
Hence Proved \boxed{\text{(ii) }\text{Area}(\triangle ABC)=\dfrac{1}{2}\times\text{Perimeter}\times r}
Section D — Long Answer Type Questions (5 marks each)
Q32. Rohan can row the boat at a speed of 5\ \text{km/hr} in still water. If it takes him 1 hour more to row the boat 5.25\ \text{km} upstream than to return downstream, find the speed of the stream.
Solution:
Step 1.
Given speed of boat in still water = 5 \text{ km/hr}.
Let stream speed = s\ \text{km/hr}.
Upstream speed of boat = 5-s.
Downstream speed of boat = 5+s.
Step 2. Time upstream minus time downstream = 1 hour.
\dfrac{5.25}{5-s}-\dfrac{5.25}{5+s}=1.
Step 3. Simplify.
5.25\cdot\frac{(5+s)-(5-s)}{(5-s)(5+s)}=1
5.25\cdot\frac{2s}{25-s^{2}}=1
\frac{10.5s}{25-s^{2}}=1
Step 4. Solve quadratic.
10.5s=25-s^{2}
s^{2}+10.5s-25=0.
Multiply by 2:
2s^{2}+21s-50=0.
2s^2 + 25s - 4s - 50 = 0
s(2s + 25) -2(2s+ 25) = 0
(s -2) (2s + 25) = 0
\implies (s-2) = 0 \quad (2s+25) = 0
\implies s = 2 \quad s = - \frac{25}{2}
Since speed cannot be negative, rejecting negative value.
s = 2
Final answer: \boxed{ \text{speed of stream is } 2\ \text{km/hr}}
Q33. The following table gives weights of standard 10 students in a school. The frequency of class 49-52 is missing. It is known that the mean of the frequency distribution is 47.2. Find the missing frequency.
| Weight (kg) | 40-43 | 43-46 | 46-49 | 49-52 | 52-55 |
| Number of Students | 31 | 58 | 60 | ? | 27 |
Solution:
Step 1. Let the missing frequency be f
Step 2: Find Class Marks
x_1 = \frac{40+43}{2} = 41.5
Similarly we can find the class mark of these classes
Step 3: Make Table
| Class Interval | Class Marks x_i | Frequency f_i | d_i = x_i - A | f_i \cdot d_i |
| 40-43 | 41.5 | 31 | -6 | -186 |
| 43-46 | 44.5 | 58 | -3 | -174 |
| 46-49 | 47.5 | 60 | 0 | 0 |
| 49-52 | 50.5 | f | 3 | 3f |
| 52-55 | 53.5 | 27 | 6 | 162 |
| Sum | 176+f | 3f - 198 |
Let Assumed mean A = 47.5
Step 4: Place values in formula and Perform calculations
Give Mean = 47.2
Using formula
A + \frac{\sum f_i \cdot x_i}{ \sum f_i} = 47.2
47.5 + \frac{3f-198}{176+f} = 47.2
\frac{3f-198}{176+f} = -0.3
\frac{198 - 3f}{176+f} = 0.3
10(198 - 3f) = 3(176 + f)
1980 -30f = 528 + 3f
1452 = 33f
f = 44
Final Answer: \boxed{\text{missing frequency } = 44 }
Q34. (i) Prove: If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
(ii) Using the theorem prove: a line through the intersection point of the diagonals of a trapezium and parallel to the base divides the non-parallel sides in the same ratio.
(i) Prove: If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
Solution:
(i)
Given: In \triangle ABC
DE \parallel BC
To Prove: \frac{AD}{DB} = \frac{AE}{EC}
Construction: Join C and D along with B and E
DF \perp AC \text{ and } EG \perp AB
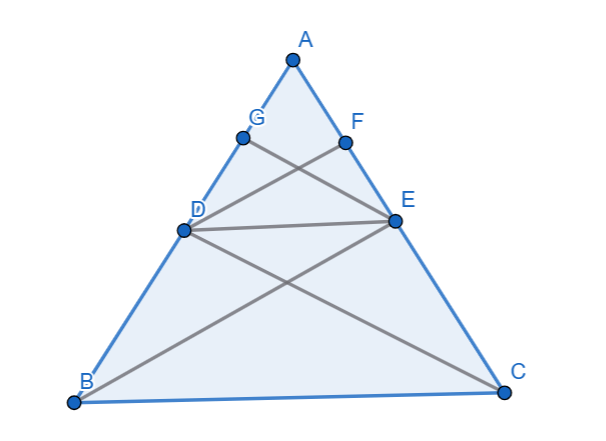
Proof:
We know Area \ of \ \triangle = \frac{1}{2} \times base \times height
Area \ of \ \triangle ADE = \frac{1}{2} \times AD \times EG
Area \ of \ \triangle ADE = \frac{1}{2} \times AE \times DF
Area \ of \ \triangle DBE = \frac{1}{2} \times DB \times EG
Area \ of \ \triangle DCE = \frac{1}{2} \times EC \times DF
\triangle DBE \ and \ \triangle DCE are on the same base DE and Between same parallel lines DE \ and \ BC .
Therefore Area \ of \ \triangle DBE = Area \ of \ \triangle DCE
\frac{Area \ of \ \triangle ADE}{Area \ of \ \triangle DBE} = \frac{Area \ of \ \triangle ADE}{Area \ of \ \triangle DCE}
Substituting values
\frac{\frac{1}{2} \times AD \times EG}{\frac{1}{2} \times DB \times EG} = \frac{\frac{1}{2} \times AE \times DF}{\frac{1}{2} \times EC \times DF}
\frac{AD}{DB} = \frac{AE}{EC}
Hence Proved: \boxed{ \text{If} \ DE \parallel BC \ \text{then} \frac{AD}{DB} = \frac{AE}{EC} }
(ii) Using the theorem prove: a line through the intersection point of the diagonals of a trapezium and parallel to the base divides the non-parallel sides in the same ratio.
Solution
(ii)
Given: ABCD is a trapezium with AB \parallel CD
And EF \parallel CD
To Prove: \frac{AE}{EC} = \frac{BF}{FD}
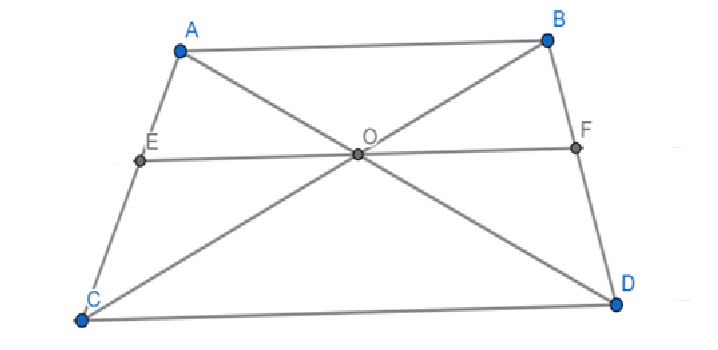
Proof:
In \triangle ACD
\because EO \parallel CD
\therefore \frac{AE}{EC} = \frac{AO}{OD} … (i) \quad \text{Using BPT}
\because EF \parallel CD and AB \parallel CD
\therefore EF \parallel AB
In \triangle DAB
\because FO \parallel AB
\therefore \frac{DF}{FB} = \frac{DO}{OA} \quad \text{Using BPT}
\rightarrow \frac{FB}{DF} = \frac{OA}{DO} … (2)
Equating (1) and (2)
\frac{OA}{DO} = \frac{FB}{DF} = \frac{AE}{EC}
Hence Proved: \boxed{ \frac{AE}{EC} = \frac{BF}{FD}}
Q35(A) . A restaurant stores ice-cream in a box with a dispenser attached for filling ice-cream cones. The dimensions of the box and the ice-cream cones used by the restaurant are shown in Figure 1 below. To make each serving of dessert, the cone is first filled with ice-cream and then topped with a hemispherical scoop of ice-cream taken from the same box, as shown in Figure 2.
Approximately how many desserts can be served out of a completely filled box of ice-cream? Show your steps. (Take \pi as \dfrac{22}{7} )
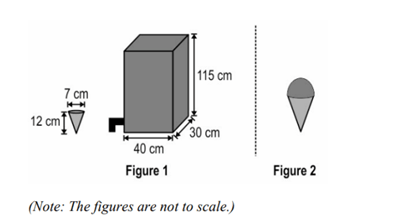
Solution:
Step 1. Volume of the rectangular box.
V_{\text{box}} = L \times B \times H
V_{\text{box}} = 40 \times 30 \times 115 = 138000\ \text{cm}^3
Step 2. Volume of one ice cream (cone + hemisphere).
Volume of cone:
V_{\text{cone}} = \dfrac{1}{3}\pi r^2 h
V_{\text{cone}} = \dfrac{1}{3}\times\dfrac{22}{7}\times {\dfrac{7}{2}}^2 \times 12
V_{\text{cone}} = \dfrac{1}{3}\times\dfrac{22}{7}\times \dfrac{49}{4} \times 12
V_{\text{cone}} = \dfrac{22 \times \frac{49}{4} \times 12}{21}
V_{\text{cone}} = 154 \ \text{cm}^3
Volume of hemisphere:
V_{\text{hemisphere}} = \dfrac{1}{2}\times\dfrac{4}{3}\pi r^3
V_{\text{hemisphere}} = \dfrac{2}{3}\pi r^3
V_{\text{hemisphere}} = \dfrac{2}{3}\times\dfrac{22}{7}\times (\dfrac{7}{2})^3
V_{\text{hemisphere}} = \dfrac{44\times\frac{343}{8}}{21}
V_{\text{hemisphere}}= 89.83 \ \text{cm}^3
Step 3. Total volume of one ice cream.
V_{\text{ice cream}} = V_{\text{cone}} + V_{\text{hemisphere}}
V_{\text{ice cream}} = 154 + 89.83
V_{\text{ice cream}} = 243.83 \ \text{cm}^3
Step 4. Number of ice creams that can be filled in the box.
\text{Number of ice creams} = \dfrac{V_{\text{box}}}{V_{\text{ice cream}}}
\text{Number of ice creams} = \dfrac{138000}{243.83}
\text{Number of ice creams} = 565.96
Final Answer: \boxed{\text{Number of ice creams that can be filled} = 565}
Q35(B). A right-circular cylindrical water tanker supplies water to colonies on the outskirts of a city and to nearby villages. Each colony has a cuboidal water tank. In villages, people come with matkas (spherical clay pots) to fill water for their household.
i) How many colonies in total would one full tanker be able to supply?
ii) If a tanker supplies water to 3 colonies and then goes to a village where 400 people fill their matkas, roughly how much water is supplied by the tanker in all?
Give your answer in m3.
Show your work.
(Note: Assume all the tanks/matkas are completely filled without any loss of water, Take π as \frac{22}{7} Use 1000000 cm3 =1 m3 .)
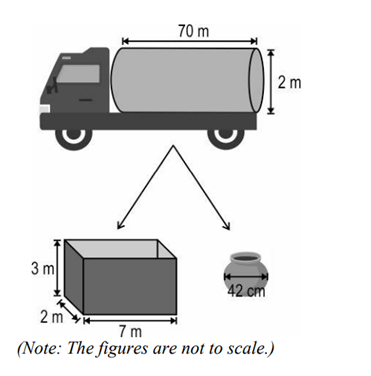
Solution:
(i) Step 1. Radius of tanker:
r=\dfrac{2}{2}=1\ \text{m}.
Step 2. Volume of tanker:
V_{\text{tanker}}=\pi r^{2}h=\pi\cdot 1^{2}\cdot 70=70\pi\ \text{m}^{3}.
Step 3. Volume of one colony tank:
V_{\text{tank}}=length \times breadth \times height
V_{\text{tank}}=7\times 2\times 3=42\ \text{m}^{3}.
Step 4. Number of tanks = \dfrac{V_{\text{tanker}}}{V_{\text{tank}}}.
Number of tankers = \dfrac{V_{\text{tanker}}}{V_{\text{tank}}}
Number of tankers = \dfrac{70\pi}{42}=\dfrac{5}{3}\pi
Number of tankers =\dfrac{5}{3}\times\dfrac{22}{7}=\dfrac{110}{21}.
Number of tankers = 5.238
Step 5. Number of full tankers is 5.
Final answer: \boxed{\text{One full tanker can supply }5\ \text{colonies completely.}}
(ii) Step 1. Volume supplied to 3 colonies.
Volume of one colony tank: V_{\text{colony}}=7\times2\times3=42\ \text{m}^3
So for 3 colonies: V_{3\ \text{colonies}}=3\times42=126\ \text{m}^3
Step 2. Volume of one matka.
Matka radius:
r_{m}=\dfrac{42\ \text{cm}}{2}=\dfrac{21}{100}\ \text{m}
Volume of one sphere:
V_{\text{matka}}=\dfrac{4}{3}\pi r_{m}^{3}=\dfrac{4}{3}\pi\left(\dfrac{21}{100}\right)^{3}
Simplify numerator:
\left(\dfrac{21}{100}\right)^{3}=\dfrac{9261}{1000000}
So
V_{\text{matka}}=\dfrac{4}{3}\pi\cdot\dfrac{9261}{1000000}=\dfrac{12348}{1000000}\pi=\dfrac{12348\pi}{10^{6}}\ \text{m}^3
Substitute \pi=\dfrac{22}{7}:
V_{\text{matka}}=\dfrac{12348}{10^{6}}\times\dfrac{22}{7}=\dfrac{271656}{7000000}=\dfrac{135828}{3500000}=\dfrac{67914}{1750000}\ \text{m}^3
Step 3. Volume for 400 matkas.
V_{400}=400\times V_{\text{matka}}=400\times\dfrac{67914}{1750000}
V_{400} =\dfrac{271656}{17500}=\dfrac{543312}{35000}
V_{400}=\dfrac{9702}{625}\ \text{m}^3
Step 4. Total volume supplied (3 colonies + 400 matkas).
V_{\text{total}} =126+\dfrac{9702}{625}=\dfrac{126\times625+9702}{625}
V_{\text{total}} =\dfrac{78750+9702}{625}=\dfrac{88452}{625}\ \text{m}^3
V_{\text{total}}=\dfrac{88452}{625}\ \text{m}^3\ =141\dfrac{327}{625}\ \text{m}^3
Final answer: \boxed{ \text{water supplied by tanker in } m^3 \ is 141 m^3}
Section E — Case Based Study Questions (1+1+2 marks each)
Q36. Answer the following questions based on the information given below.
Ms. Sheela visited a store near her house and found that the glass jars are arranged one above the other in a specific pattern. On the top layer there are 3 jars.
In the next layer there are 6 jars. In the 3rd layer from the top there are 9 jars and so on till the 8th layer.
(i) Write an A.P whose terms represent the number of jars in different layers starting from top . Also, find the common difference.
(ii) Is it possible to arrange 34 jars in a layer if this pattern is continued? Justify your answer.
(iii) (A) If there are ‘n’ number of layers then find the expression for finding the total number of jars in terms of n. Hence find .
OR
(iii) (B) The shopkeeper added 3 jars in each layer. How many jars are there in the 5th layer from the top?
(i) Write an A.P whose terms represent the number of jars in different layers starting from the top. Also, find the common difference.
Solution:
The number of jars in each layer:
3,\ 6,\ 9,\ 12,\ 15,\ 18,\ 21,\ 24
So,
First term a = 3
Common difference d = 6 - 3 = 3
Final Answer: \boxed{\text{A.P: } 3,6,9,12,15,18,21,24\quad \text{and } d = 3}
(ii) Is it possible to arrange 34 jars in a layer if this pattern is continued? Justify your answer.
Solution:
General term of A.P:
a_n = a + (n-1)d
a_n = 3 + (n-1)\times 3 = 3n
If there are 34 jars,
3n = 34 \Rightarrow n = \dfrac{34}{3} = 11\dfrac{1}{3}
Since n is not a natural number,
it is not possible to have a layer with 34 jars.
Final Answer: \boxed{\text{No, because } n = 11\dfrac{1}{3}\text{ is not a natural number.}}
(iii)(A) If there are ‘n’ number of layers then find the expression for finding the total number of jars in terms of n. Hence find S_8.
Solution:
Sum of n terms of A.P:
S_n = \dfrac{n}{2},[2a + (n-1)d]
Substitute a = 3, d = 3:
S_n = \dfrac{n}{2}[2(3) + (n-1)3]
S_n = \dfrac{n}{2},[6 + 3n - 3]
S_n = \dfrac{n}{2},(3n + 3)
S_n= \dfrac{3n(n+1)}{2}
Now find S_8:
S_8 = \dfrac{3\times 8\times 9}{2} = 3\times 36 = 108
Final Answer: \boxed{S_n = \dfrac{3n(n+1)}{2},\quad S_8 = 108\text{ jars}}
(iii)(B) The shopkeeper added 3 jars in each layer. How many jars are there in the 5th layer from the top?
Solution:
Old 5th term = a_5 = 3 + (5-1)\times 3 = 15
After adding 3 jars per layer:
a_5 = 15 + 3 = 18
Final Answer: \boxed{\text{There will be 18 jars in the 5th layer.}}
Q37. Answer the following questions based on the information given below.
A drone, is an aircraft without any human pilot and is controlled by a remote-control device. Its various applications include policing, surveillance, photography, precision agriculture, forest fire monitoring, river monitoring and so on.
David used an advanced drone with high resolution camera during an expedition in a forest region which could fly upto 100 m height above the ground level. David rode on an open jeep to go deeper into the forest. The initial position of drone with respect to the open jeep on which David was riding is shown below

David’s jeep started moving to enter the forest at an average speed of 10 m/s. He Simultaneously started flying the drone in the same direction as that of the jeep. (take as 1.73)
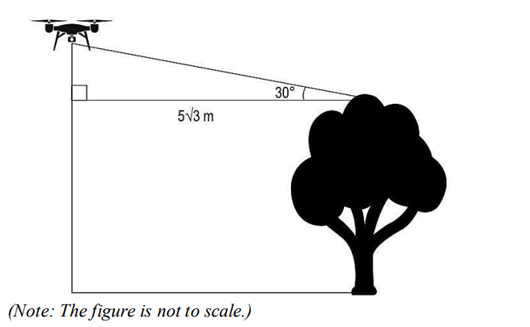
(i) David reached near one of the tallest trees in the forest. He stopped the drone at a horizontal distance of 5√3 m from the top of the tree and at a vertical distance of 65 m below its maximum vertical range. If the angle of elevation of the drone from the top of the tree was 30°, find the height of the tree. Show your work.
(ii) The drone was flying at a height of metres at a constant speed in the horizontal direction when it spotted a zebra near a pond, right below the drone.
The drone travelled for 30 metres from there and it could see the zebra, at the same place, at an angle of depression of θ from it. Draw a diagram to represent this situation and find θ. Show you work.
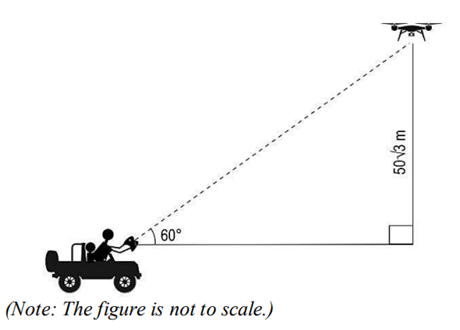
(iii) (A) After 2 minutes of starting the expedition both the drone and the jeep stopped at the same moment so that the drone can capture some images. The position of the drone and the jeep when they stopped is as shown below. Find the average speed of the drone in m/s rounded off upto 2 decimal places. Show your work.
OR
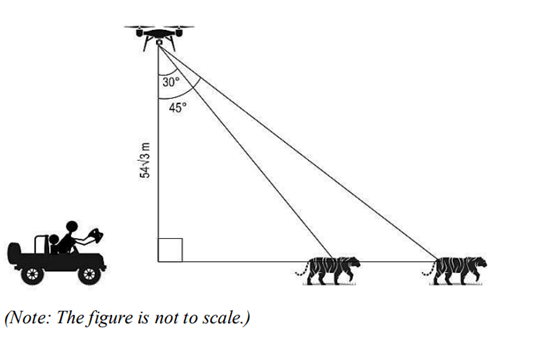
(B) At some point during the expedition, David kept the drone stationary for some time to capture the images of a tiger. The angle of depression from the drone to the tiger changed from 30° to 45° in 3 seconds as shown below. What was the average speed of the tiger during that time? Show your work.
(i) David reached near one of the tallest trees in the forest. He stopped the drone at a horizontal distance of 5√3 m from the top of the tree and at a vertical distance of 65 m below its maximum vertical range. If the angle of elevation of the drone from the top of the tree was 30°, find the height of the tree. Show your work.
Solution:
Tree: CD
Drone at E.
Maximum Vertical Range of Drone= 100m
Height of Drone: EA = 100 - 65 = 35 m
In \triangle BCE
\tan 30^\circ = \frac{BE}{BC}
\frac{1}{\sqrt{3}} = \frac{BE}{5\sqrt{3}}
BE = 5 \ m
BA = AE - BE
BA = 35 - 5
BA = 30 \ m
CD = BA = 30 \ m
CD = 30 \ m
Final Answer: \boxed { \text{Height of the tree is } 30 \ m}
(ii) The drone was flying at a height of metres at a constant speed in the horizontal direction when it spotted a zebra near a pond, right below the drone.
The drone travelled for 30 metres from there and it could see the zebra, at the same place, at an angle of depression of θ from it. Draw a diagram to represent this situation and find θ. Show you work.
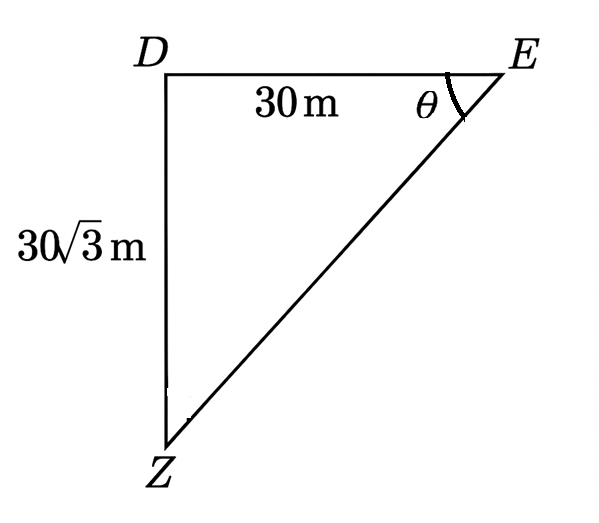
Solution:
Zebra at Z
Initial Position of drone D
Final Position of drone E
In \triangle DEZ
\tan \theta = \frac{DZ}{DE}
\tan \theta = \frac{30 \sqrt{3}}{3}
\tan \theta = \sqrt{3}
\tan \theta = \tan 60^\circ
\theta = 60^\circ
Final Answer: \boxed{ \theta = 60^\circ}
(iii) (A) After 2 minutes of starting the expedition both the drone and the jeep stopped at the same moment so that the drone can capture some images. The position of the drone and the jeep when they stopped is as shown below. Find the average speed of the drone in m/s rounded off upto 2 decimal places. Show your work.
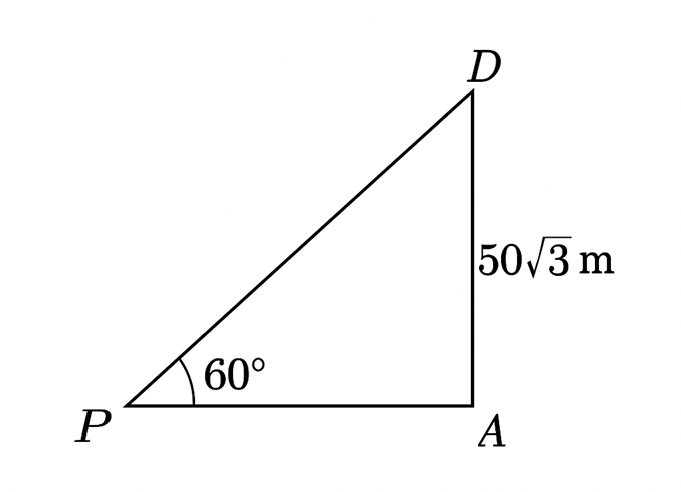
Solution:
Final Position of drone: D
Initial Horizontal distance between David and drone = 0m
Final Horizontal distance between David and drone = PA
Speed of David = 10 m/sec
Let the speed of the drone be x.
Relative speed of drone w.r.t. David = (x-10) m/sec
Time Travelled = 2 min = 120 sec
In \triangle PAD
\tan 60^\circ = \frac{AD}{PA}
\sqrt{3} = \frac{50 \sqrt{3}}{PA}
PA = 50 \ m
Since speed = \frac{distance}{time}
speed = \frac{distance}{time}
x - 10 = \frac{50}{120}
x - 10 = 0.416
x = 10.416
x = 10.42 \ m/sec
Final Answer: \boxed{ \text{The speed of the drone is } 10.42 \text{ m/sec} }
(B) At some point during the expedition, David kept the drone stationary for some time to capture the images of a tiger. The angle of depression from the drone to the tiger changed from 30° to 45° in 3 seconds as shown below. What was the average speed of the tiger during that time? Show your work.
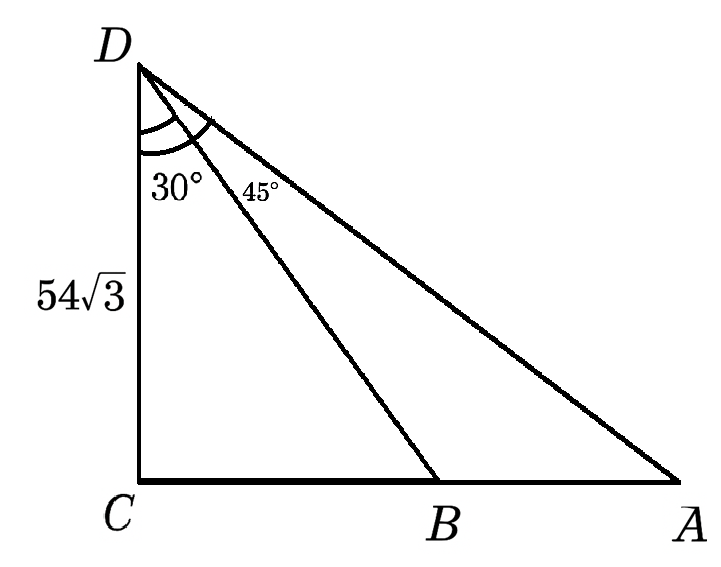
Solution:
Drone at D
Initial position of drone: B
Final position Position of drone: A
Time Taken by tiger to travel from B to A = 3 secs
Height to drone DC= 54 \sqrt{3}
In \triangle ACD
\tan D = \frac{AC}{DC}
\tan 45^{\circ} = \frac{AC}{54 \sqrt{3}}
1 = \frac{AC}{54 \sqrt{3}}
54 \sqrt{3} = AC
In \triangle BCD
\tan D = \frac{BC}{DC}
\tan 30^{\circ} = \frac{BC}{54 \sqrt{3}}
\frac{1}{\sqrt{3}} = \frac{BC}{54 \sqrt{3}}
\frac{54 \sqrt{3}}{\sqrt{3}} = BC
BC = 54
Distance travelled by tiger AB = AC - BC = 54 \sqrt{3} - 54
AB = 54 (\sqrt{3} - 1)
\text {Speed of tiger} = \frac{distance}{time}
\text {Speed of tiger} = \frac {AB}{3}
\text {Speed of tiger} = \frac{54 (\sqrt{3} - 1)}{3}
\text {Speed of tiger} = 18 (\sqrt{3} - 1) \text{m/sec}
\text {Speed of tiger} = 18 (1.73 - 1) \text{m/sec}
\text {Speed of tiger} = 18 (0.73) \text{m/sec}
\text {Speed of tiger} = 13.14 \text{m/sec}
Final Answer: \boxed{ \text {The speed of tiger is } 13.14 \text{m/sec} }
Q38. Answer the following questions based on the information given below.
Raycasting is a technique used in the creation of computer games. The basic idea of raycasting is as follows: the map is a 2D square grid. Using rays generated from an object, this 2D map can be transformed into a 3D perspective. One of the methods involves sending out a ray from the player’s location. To determine how far he/she is from a wall or an obstacle, the distance between the player’s coordinates and the coordinate of the wall is calculated. If the player is near the obstacle, it looks larger and vice-versa.
Shown below is a game, Wolf 3D, which was created using raycasting.
Riju wants to create an online snooker game using raycasting. The game in the creation stage on a coordinate map is shown below.
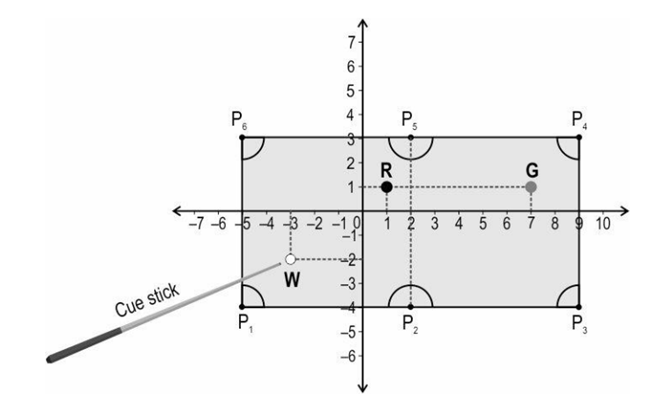
The snooker table has six pockets (P1, P2, P3, P4, P5 and P6) and he has shown three balls – white (W), red (R) and green (G) on the table. The objective of the game is to use the white ball to hit the coloured balls into the pockets using a cue stick.
(i) How much distance will a ray travel if sent from the green ball to the nearest pocket? Show your work.
(ii) Riju wants to place a yellow ball at the midpoint of the line connecting the white and green balls. Find the coordinates of the point at which he should place the yellow ball. Show your steps.
(iii) (A) Riju is running a trial on his game. He struck the white ball in a way that it rebound off the rail (line connecting P4 and P6) and went into the pocket P2.
♦ After the rebound, the ball crossed the x-axis at point X( 2/7 , 0) on the way to the pocket.
♦ The ratio of the distance between the rail and point X and the distance between point X and the pocket was 3:4.
Find the coordinates of the point at which the ball struck the rail. Show your steps.
OR
(iii) (B) Riju wants to hit a blue ball placed at (-1, -3) into pocket P5 along a straight path. Would the red ball lie on the straight path between the blue ball and P5? Justify your answer.
Solution:
Plotting the important Points on the coordinate plane
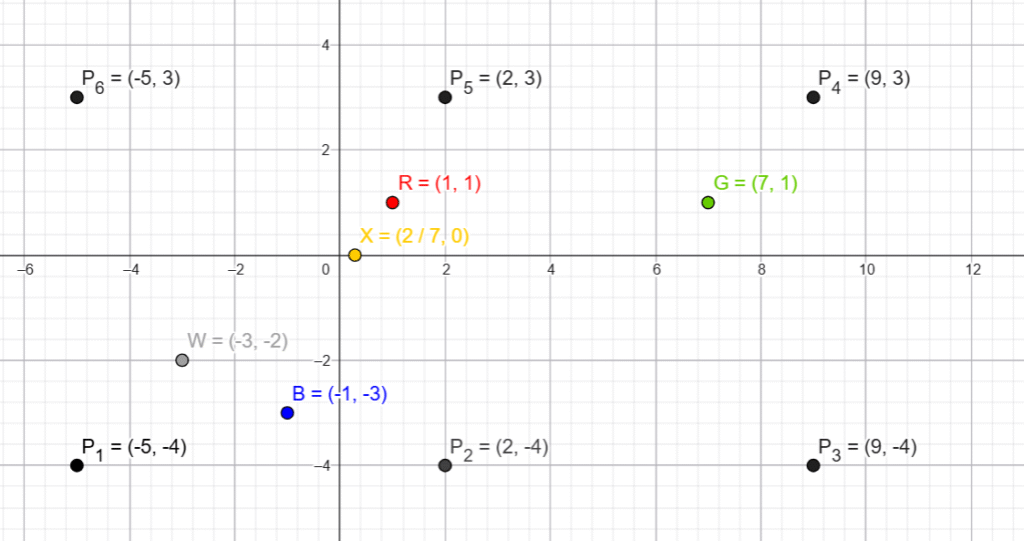
(i) How much distance will a ray travel if sent from the green ball to the nearest pocket? Show your work.
Solution:
The Pocket nearest to the Green ball is P4
Distance from G to P4 = \sqrt{ (x_2 - x_1)^2 + (y_2 - y_1)^2 }
Distance from G to P4 = \sqrt{ (9 - 7)^2 + (3 - 1)^2 }
Distance from G to P4 = \sqrt{ (2)^2 + (2)^2 }
Distance from G to P4 = \sqrt{ 8 }
Distance from G to P4 = 2\sqrt{ 2 }
Final Answer: \boxed{ \text{Distance of ray will be} = 2\sqrt{ 2 } }
(ii) Riju wants to place a yellow ball at the midpoint of the line connecting the white and green balls. Find the coordinates of the point at which he should place the yellow ball. Show your steps.
Solution:
Coordinates of Yellow Ball Y (x,y) = Mid point formula between White (-3, -2) and Green (7, 1) Balls
x = \frac{x_1 + x_2}{2}
x = \frac{-3 + 7}{2}
x = \frac{4}{2}
x = 2
Now for y coordinate
y = \frac{y_1 + y_2}{2}
y = \frac{-2 + 1}{2}
y = \frac{-1}{2}
Final Answer: \boxed{ \text{We should place the yellow ball at } Y(2, \frac{-1}{2}) }
(iii)(A). Riju is running a trial on his game. He struck the white ball in a way that it rebound off the rail (line connecting P4 and P6) and went into the pocket P2.
♦ After the rebound, the ball crossed the x-axis at point X( 2/7 , 0) on the way to the pocket.
♦ The ratio of the distance between the rail and point X and the distance between point X and the pocket was 3:4.
Find the coordinates of the point at which the ball struck the rail. Show your steps.
Solution:
Let the Point at which the ball struck the rail be S(x_1, y_1)
Given that the point X(\frac{2}{7}, 0 ) divides S(x_1, y_1) and P_2(2, -4) in the ratio 3:4.
Applying Section formula
x = \frac{m_1 x_2 + m_2 x_1}{m_1 + m_2}
\frac{2}{7} = \frac{3 \cdot 2 + 4 x_1}{3 + 4}
\frac{2}{7} = \frac{6 + 4 x_1}{7}
2 = 6 + 4 x_1
-4 = 4 x_1
x_1 = -1
Now for y coordinate
y = \frac{m_1 y_2 + m_2 y_1}{m_1 + m_2}
0 = \frac{3 \cdot (-4) + 4 y_1}{3 + 4}
0 = \frac{-12 + 4 y_1}{7}
0 = -12 + 4 y_1
12 = 4 y_1
y_1 = 3
The point Where the Ball struck the Rail is S(-1, 3)
Final Answer: \text{The final point where the ball struck the rail is } S(-1, 3)
(iii)(B). Riju wants to hit a blue ball placed at (-1, -3) into pocket P5 along a straight path. Would the red ball lie on the straight path between the blue ball and P5? Justify your answer.
Solution:
We have to check if Blue ball, Red ball and P5 pocket, lie on a straight line?
In other words, we have to check if B(-1, -3), R(1, 1) and P5(2,3) are collinear?
Calculate the Distance Between BR using Distance Formula
BR = \sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2}
BR = \sqrt {(1 - (-1))^2 + (1 - (-3))^2}
BR = \sqrt {(2)^2 + (4)^2}
BR = \sqrt {20}
BR = 2\sqrt {5}
Calculate the Distance Between RP5 using Distance Formula
RP_{5} = \sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2}
RP_{5} = \sqrt {(3 - 1)^2 + (2 - 1)^2}
RP_{5} = \sqrt {(2)^2 + (1)^2}
RP_{5} = \sqrt {5}
Calculate the Distance Between BP5 using Distance Formula
BP_{5} = \sqrt {(x_2 - x_1)^2 + (y_2 - y_1)^2}
BP_{5} = \sqrt {(3 - (-3))^2 + (2 - (-1))^2}
BP_{5} = \sqrt {(6)^2 + (3)^2}
BP_{5} = \sqrt {36 + 9}
BP_{5} = \sqrt {45}
BP_{5} = 3\sqrt {5}
BR + RP_{5} = 2\sqrt {5} + \sqrt {5} = 3\sqrt {5} = BP_{5}
BR + RP_{5} = BP_{5}
Therefore We can say B(-1, -3), R(1, 1) and P5(2,3) are collinear
Final Answer: \boxed{ \text { Yes, the red ball lie on the straight path between the blue ball and Pocket } P_5 }
Class 10 Full Syllabus Practice Question Paper-1 2026 ⇒
Summary
This post provides full Class 10 CBSE Maths Practice Paper 2026 Solutions with detailed explanations from Sections A to E. Students can strengthen concepts, revise efficiently, and download the PDF version for offline study before the board exam.
Important Links
Class 12th CBSE Official Sample Papers and Marking Schemes
Class 10th CBSE Official Sample Papers and Marking Schemes
Class 12th ISC Official Specimen Papers and Answer Keys
Class 11th ISC Official Specimen Papers and Answer Keys
Class 10th ICSE Official Specimen Papers and Answer Keys
Class 9th ICSE Official Specimen Papers and Answer Keys