Intoduction
Have you solved Class 10 CBSE Maths Practice Paper-2 2026 and are looking for a solutions to the questons? Here you’ll find complete, step-by-step NCERT-style solutions for every question. Designed for both students and teachers, these answers make board exam revision easier with clear explanations, formula highlights, and downloadable PDF options.
Class 10 Full Syllabus Practice Question Paper-2 2026 ⇒
Solution to the paper
Section A — Multiple Choice Questions (1 mark each)
Q1. Which of the following is a solution to the equation 2x^2+13x-7=0?
Options: (A) 2 (B) -1 (C) -7 (D) \frac{1}{2}
Solution:
Step 1. Substituting options in eq: 2x^2+13x-7=0
For x=-7 \Rightarrow 2(49)-91-7=0.
LHS = RHS i.e. equations is satisfied by -7
Therefore -7 is a solution of the given equation
✅ Correct Option: (C)
Q2. If a, b, c, d, e, f are in A.P., find e - c.
Options: (A) 2(c-a) (B) 2(f-d) (C) 2(d-c) (D) d-c
Solution:
Write the AP terms:
a=a, \ b= a+d, \ c= a+2d, \ d= a+3d, \ e = a+4d, \ f = a+5d
Therefore,
e-c = (a+4r) - (a+2r) = 2r
Also,
d-c = (a+3r) - (a+2r) = r
Thus,
e-c = 2(d-c)
✅ Correct Option: (C)
Q3. In the figure, if O is centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50^\circ with PQ, then \angle POQ is equal to:
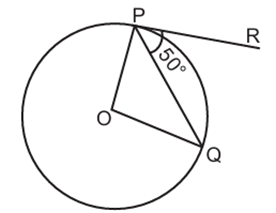
Options: (A) 100^\circ (B) 80^\circ (C) 90^\circ (D) 75^\circ
Solution:
\angle OPR = 90^\circ \quad … (radius meets the tangent at 90o)
\angle OPQ + \angle RPQ = 90^\circ
\angle OPQ + 50^\circ = 90^\circ
\angle OPQ = 40^\circ
In \triangle OPQ
\because OP = OQ \quad … (radii)
\therefore \angle OPQ = \angle OQP
\therefore \angle OPQ = 40^\circ
In \triangle OPQ
\angle OPQ + \angle OQP + \angle POQ = 180^\circ \quad … (Angle sum prop of a triangle)
40^\circ + 40^\circ + \angle POQ = 180^\circ
100^\circ + \angle POQ = 180^\circ
\angle POQ = 80^\circ
✅ Correct Option: (B)
Q4. The graph of a polynomial p(x) passes through the points (-8,0), (0,-10), (4,-20) and (6,0). The zeroes of the polynomial are
Options: (A) 6, 0 (B) 4, 6 (C) -10, -20 (D) -8, -6
Solution:
If the graph touches x-axis at x=-8 and x=6,
then the polynomial has zeros: -8 \text{ and } 6
✅ Correct Option: (D)
Q5. The shape of a gilli, in the gilli-danda game (see Fig.), is a combination of

Options:
(A) two cylinders
(B) a cone and a cylinder
(C) two cones and a cylinder
(D) two cylinders and a cone
Solution:
The typical shape consists of:
• A cylinder at the centre
• Two cones on each side (pointed ends)
So,
\text{Gilli} = \text{Cylinder + Two Cones}
✅ Correct Option: (C)
Q6. If Mean = 24 and Median = 26, then Mode is:
Options: (A) 23 (B) 26 (C) 25 (D) 30
Solution:
Using formula:
\text{Mode} = 3 \times \text{Median} - 2 \times \text{Mean}
\text{Mode} = 3(26) - 2(24)
\text{Mode} = 78 - 48 = 30
✅ Correct Option: (D)
Q7. The point which divides the line segment of points P(-1, 7) and Q(4, -3) in the ratio of 2:3 is:
Options: (A) (-1, 3) (B) (-1, -3) (C) (1, -3) (D) (1, 3)
Solution:
By section formula,
\left(x,y\right) = \left(\dfrac{2\cdot 4+3\cdot(-1)}{2+3},\dfrac{2\cdot(-3)+3\cdot 7}{2+3}\right)
\left(x,y\right) =\left(\dfrac{8-3}{5},\dfrac{-6+21}{5}\right)
\left(x,y\right)=(1,3)
✅ Correct Option: (D)
Q8. In the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid
points of sides AB, BC, CD and DA respectively. The area of the shaded portion is
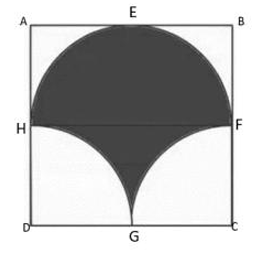
Options: (A) 44\text{ cm}^2 (B) 49\text{ cm}^2 (C) 98\text{ cm}^2 (D) 44 \frac{\pi}{2}\text{ cm}^2
Solution:
Area of the shaded portion = Half the area of original square.
\text{Shaded Area}=\dfrac{1}{2}\times 14^2=\dfrac{196}{2}=98\text{ cm}^2
✅ Correct Option: (C)
Q9. A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then the distance by which the top of the ladder would slide upwards on the wall is:
Options: (A) 2 m (B) 1.2 m (C) 0.8 m (D) 0.5 m
Solution:
Initial foot distance: \sqrt{5^2-4^2}=3 m.
New foot distance: 3-1.6=1.4 m.
New height: \sqrt{5^2-1.4^2}=\sqrt{25-1.96}=4.8 m.
Rise: 4.8-4=0.8 m.
✅ Correct Option: (C)
Q10. If \cot A=\dfrac{5}{6}, then \dfrac{3\cos A+\sin A}{\sin A-6\cos A} is equal to:
Options: (A) \frac{7}{8} (B) -\frac{7}{8} (C) -\frac{5}{4} (D) \frac{5}{4}
Solution:
Let y = \dfrac{3\cos A+\sin A}{\sin A-6\cos A}
dividing numerator and denominator by \sin A
y = \dfrac{ 3 \cdot\frac{\cos A}{\sin A}+ \frac{\sin A}{\sin A}}{ \frac{\sin A}{\sin A}- 6 \cdot \frac{\cos A}{\sin A}}
y = \dfrac{ 3\cot A+ 1}{ 1 - 6\cot A}
Substituting
\cot A=\dfrac{5}{6}
y = \dfrac{ 3\cdot \frac{5}{6}+ 1}{ 1 - 6 \cdot \frac{5}{6}}
y = \dfrac{ \frac{5}{2}+ 1}{ 1 - 5}
y = \dfrac{ \frac{7}{2}}{-4}
y = -\dfrac{7}{8}
✅ Correct Option: (B)
Q11. AOBC is a rectangle whose three vertices are A(0,3), O(0,0) and B(5,0). The length of the diagonal is
Options: (A) 5 (B) 3 (C) \sqrt{34} (D) 4
Solution:
Diagonal = AB
Using distance formula
AB = \sqrt{(5-0)^2+(0-3)^2}
AB = \sqrt{25+9}
AB =\sqrt{34}
✅ Correct Option: (C)
Q12. Two fair dice are thrown simultaneously. The probability of getting a doublet is:
Options: (A) \frac{1}{36} (B) \frac{1}{6} (C) \frac{5}{6} (D) \frac{11}{36}
Solution:
Favourable outcomes: (1,1) \ (2,2) \ (3,3) \ (4,4) \ (5,5) \ (6,6) → 6.
Total number of outcomes: 36.
Probability of getting a doublet : \dfrac{6}{36}=\dfrac{1}{6}.
✅ Correct Option: (B)
Q13. If a tower 6\text{ m} high casts a shadow of 2\sqrt{3}\text{ m} long on the ground, then the sun’s elevation is:
Options: (A) 60^\circ (B) 45^\circ (C) 30^\circ (D) 90^\circ
Solution:
\tan\theta=\dfrac{6}{2\sqrt{3}}=\sqrt{3}
\Rightarrow \theta=60^\circ.
✅ Correct Option: (A)
Q14. In the given figure, find the value of x in terms of a, b and c.
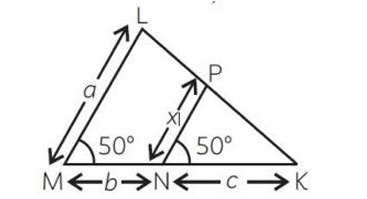
Options: (A) \frac{ac}{b+c} (B) \frac{ab}{b+c} (C) \frac{ac}{b} (D) \frac{ab}{c}
Solution:
\triangle KPN \sim \triangle KLM
\dfrac{KN}{KM} = \dfrac{NP}{ML} =\dfrac{KP}{KL}
Considering ony \dfrac{KN}{KM} = \dfrac{NP}{ML}
\dfrac{c}{b+c} = \dfrac{x}{a}
\dfrac{ac}{b+c}= x
x = \dfrac{ac}{b+c} .
✅ Correct Option: (A)
Q15. The pair of linear equations 2x+3y=5 and 4x+6y=10 is
Options: (A) Inconsistent (B) Consistent (C) Dependent Consistent (D) None of these
Solution:
For, 2x+3y=5 \quad a_1 = 2 \ b_1 = 3 \ c_1 = 5
For, 4x+6y=10 \quad a_2 = 4 \ b_2 = 6 \ c_2 = 10
\dfrac{a_1}{a_2} = \dfrac{2}{4} = \dfrac{1}{2}
\dfrac{b_1}{b_2} = \dfrac{3}{6} = \dfrac{1}{2}
\dfrac{c_1}{c_2} = \dfrac{5}{10} = \dfrac{1}{2}
i.e. \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2}
\therefore The the pair of linear equations has Infinitely many solutions.
System is consistent and dependent.
✅ Correct Option: (C)
Q16. In trapezium ABCD with AD\parallel BC and AD=4\text{ cm}, diagonals intersect at O with \dfrac{AO}{OC}=\dfrac{DO}{OB}=\dfrac{1}{2}. Then BC equals:
Options: (A) 6 (B) 7 (C) 8 (D) 9
Solution:
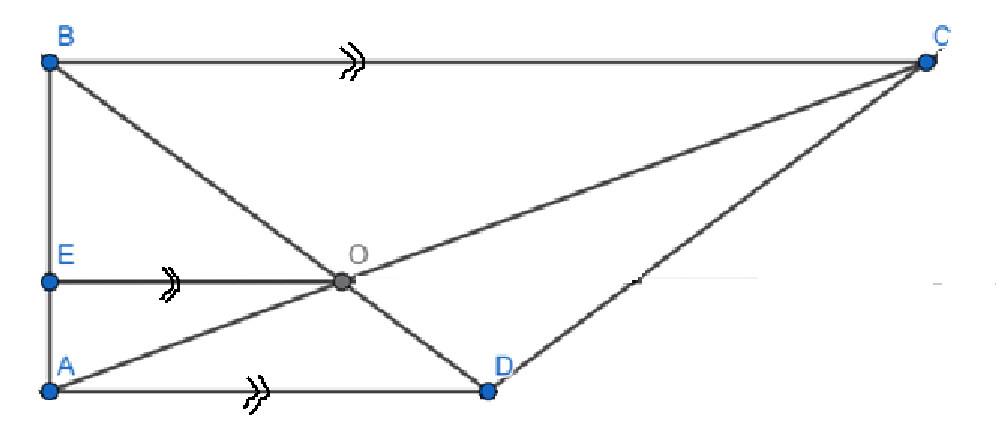
Given:
ABCD is a trapezium with AD \parallel BC
AD = 4\text{ cm}
\frac{AO}{OC} = \frac{DO}{BO} = \frac{1}{2}
Construction: Draw EO parallel to BC
To find: BC
\triangle BEO \sim \triangle BAD
\therefore \frac{BO}{BD} = \frac{EO}{AD} … (1)
We know \frac{DO}{BO} = \frac{1}{2}
Adding 1 to both sides
\frac{DO}{BO} + 1 = \frac{1}{2} + 1
\frac{DO+BO}{BO} = \frac{3}{2}
\frac{DO+BO}{BO} = \frac{3}{2}
\frac{BD}{BO} = \frac{3}{2}
Substituting in (1)
\frac{2}{3} = \frac{EO}{AD}
\frac{2}{3} = \frac{EO}{4}
\frac{8}{3} = EO
\triangle AEO \sim \triangle ABC
\therefore \frac{AO}{AC} = \frac{EO}{BC} … (2)
We know \frac{AO}{OC} = \frac{1}{2} \implies \frac{OC}{AO} = \frac{2}{1}
Adding 1 to both sides
\frac{OC}{AO} + 1 = \frac{2}{1} + 1
\frac{OC+AO}{AO} = \frac{3}{1}
\frac{AC}{AO} = 3
Substituting in (2)
\frac{1}{3} = \frac{EO}{BC}
Substituting EO
\frac{1}{3} = \frac{8}{3 \times BC}
BC = 8
✅ Correct Option: (C)
Q17. The probability than a non-leap year selected at random will contain 53 Sundays is:
Options: (A) \frac{1}{7} (B) \frac{2}{7} (C) \frac{3}{7} (D) \frac{5}{7}
Solution:
A non-leap year has 365 days = 52 weeks + 1 day.
Extra day is equally likely among 7 days. (Mon, Tue, Wed, Thu, Fri, Sat, Sun)
Probability = \dfrac{1}{7}.
✅ Correct Option: (A)
Q18. The surface areas of two spheres are in the ratio 1 : 2. The ratio of their volume is:
Options: (A) \sqrt{2}:1 (B) 1:2\sqrt{2} (C) 1:8 (D) 1:4
Solution:
Given
\dfrac{S_1}{S_2} = \dfrac{1}{2}
\dfrac{4\pi {r_1}^2}{4\pi {r_2}^2} = \dfrac{1}{2}
\dfrac{{r_1}^2}{{r_2}^2} = \dfrac{1}{2}
\dfrac{r_1}{r_2} = \dfrac{1}{\sqrt{2}}
Calculating
\dfrac{V_1}{V_2} = \dfrac{\frac{4}{3} \pi {r_1}^3}{\frac{4}{3} \pi {r_2}^3}
\dfrac{V_1}{V_2} = \dfrac{{r_1}^3}{{r_2}^3}
\dfrac{V_1}{V_2} = \left( \dfrac{r_1}{r_2} \right)^3
Substituting
\dfrac{V_1}{V_2} = \left( \dfrac{1}{\sqrt{2}} \right)^3
\dfrac{V_1}{V_2} = \dfrac{1}{2\sqrt{2}}
V_1 : V_2 = 1:2\sqrt{2}
✅ Correct Option: (B)
Q19. Assertion (A): L.C.M. and H.C.F. of a and 20 are 100 and 10 respectively, then a = 50.
Reason (R): L.C.M x H.C.F. = First number x Second number
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
Solution:
a=\dfrac{100\times 10}{20}=50.
Both A and R are true and R explains A.
✅ Correct Option: (A)
Q20. Assertion (A): \sin^2 59^\circ+\cos^2 59^\circ=1.
Reason (R): For any angle A, \sin^2 A+\cos^2 A=1.
(A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(C) Assertion (A) is true but Reason (R) is false.
(D) Assertion (A) is false but Reason (R) is true.
Solution:
Identity \sin^2 A+\cos^2 A=1 holds for all real A.
R is true and explains A.
✅ Correct Option: (A)
Section B — 2 marks Questions
Q21. A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60^\circ with the wall, then find the height of the wall. Give your answer upto 1 decimal place.
(take \sqrt{3}=1.73).
Solution:
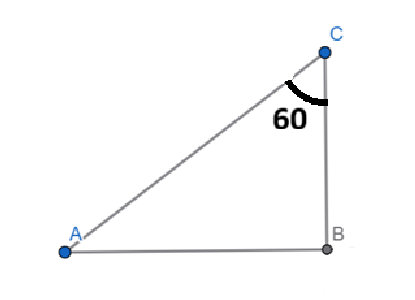
Let, Ladder: AC, Wall: BC
In \triangle ABC
\cos C = \dfrac{BC}{AC}
\cos 60^\circ=\dfrac{BC}{15}
BC = 15 \cdot \cos 60^\circ[latex] BC =7.5
\text{height of wall}=7.5
Final Answer: \boxed{\text{The height of the wall is } 7.5 \text{ m}}
Q22 (A). If the 7^{\text{th}} and 9^{\text{th}} terms of an A.P. are -33 and -25 respectively, what is its 8^{\text{th}} term?
Solution:
Let, first term: a, common difference: d
a_7=a+6d=-33 ... (1)
a_9=a+8d=-25 ... (2)
Subtracting (1) from (2)
(a+8d)-(a+6d)=(-25)-(-33)
2d=8
d=4
Substituting d in (1)
a=a_7-6d=-33-24=-57
Finding 8th term
a_8=a+7d=-57+28=-29
Final Answer: \boxed{a_8 = -29}
Q22 (B). Check whether – 150 is a term of the AP: 11, 8, 5, 2 . . . .
Solution:
Step 1. Identify the first term and common difference
a = 11,\quad d = 8 - 11 = -3
Step 2. General term of an A.P.
a_n = a + (n - 1)d
Step 3. Substitute a_n = -150
-150 = 11 + (n - 1)(-3)
Step 4. Simplify
-150 = 11 - 3(n - 1)
-150 = 11 - 3n + 3
-150 = 14 - 3n
Step 5. Solve for n
-3n = -164
n = \dfrac{164}{3} \approx 54.67
Since n is not an integer, -150 is not a term of the A.P.
Final Answer: \boxed{\text{–150 is not a term of the given A.P.}}
Q23. Prove that 4+\sqrt{3} is irrational given that \sqrt{3} is irrational.
Solution:
Assume, for contradiction, 4+\sqrt{3} is rational.
4+\sqrt{3} = \frac{a}{b} \quad \text{where } a,b \in Z \text{ and } b \neq 0
\sqrt{3} = \frac{a}{b} - 4 \quad
\sqrt{3} = \frac{a-4b}{b} \quad
\because a, b \in Z
\therefore a-4b, b \in Z
\implies \sqrt{3} \text{ is rational}
But is is given that \sqrt{3} \text{ is irrational}
This contradiction arises because of our wrong assumption.
Therefore, 4+\sqrt{3} is irrational. Hence Proved
Q24. The length of the minute hand of a clock is 10.5\text{ cm}. Find the area swept by it when it moves from 5{:}03\ \text{a.m.} to 5{:}53\ \text{a.m.}.
Solution:
The region swept by the minute hand will be a sector
Radius: r=10.5\ \text{cm}, time moved: 50\ \text{min}
Angle covered in \text{1 min} = 6^\circ
Angle covered in \text{50 mins} = \theta=50\times 6^\circ=300^\circ
\text{Area}=\dfrac{\theta}{360^\circ}\pi r^2
\text{Area}=\dfrac{300}{360}\pi(10.5)^2
\text{Area}=\dfrac{300}{360} \cdot \frac{22}{7} \cdot \frac{105}{10} \times \frac{105}{10}
\text{Area}=\dfrac{28875}{100}
\text{Area}=288.75 \text{cm}^2
Final Answer: \boxed{ \text{The area swept by the minute hand is 288.75 } \text{cm}^2 }
Q25 (A). Show that the points A(2,4),\ B\left(5,\ 4+3\sqrt{3}\right),\ C(8,4) are the vertices of an equilateral triangle.
Solution:
Using distance formula Compute side lengths:
AB=\sqrt{(5-2)^2+\left(4+3\sqrt{3}-4\right)^2}
AB=\sqrt{3^2+\left(3\sqrt{3}\right)^2}
AB=\sqrt{9+27}
AB=\sqrt{36}
AB=6
BC=\sqrt{(8-5)^2+\left(4-(4+3\sqrt{3})\right)^2}
BC=\sqrt{3^2+\left(-3\sqrt{3}\right)^2}
BC=\sqrt{9+27)^2}
BC=6
AC=\sqrt{(8-2)^2+(4-4)^2}
AC=\sqrt{6^2}
AC=6
All three sides equal, so triangle ABC is equilateral.
Final Answer: \boxed{\text{Yes, } \triangle ABC \text{ is equilateral with side } 6}
Q 25 (B) Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution:
Let the Points be P(x, y), \ A(7, 1) \ B(3, 5)
Given Equidistant \implies PA = PB
Step 1. Using distance formula.
\sqrt{(x - 7)^2 + (y - 1)^2} = \sqrt{(x - 3)^2 + (y - 5)^2}
Step 2. Square both sides to remove the square roots.
(x - 7)^2 + (y - 1)^2 = (x - 3)^2 + (y - 5)^2
Step 3. Expand both sides.
x^2 - 14x + 49 + y^2 - 2y + 1 = x^2 - 6x + 9 + y^2 - 10y + 25
Step 4. Cancel x^2 and y^2 from both sides.
-14x - 2y + 50 = -6x - 10y + 34
Step 5. Simplify.
-14x + 6x - 2y + 10y = 34 - 50
-8x + 8y = -16
Step 6. Divide by 8.
y - x = -2
Final Answer: \boxed{y = x - 2}
Section C — 3 marks Questions
Q26. If 𝛼 and 𝛽 are the zeroes of the polynomial 3𝑥² − 8𝑥 + 2, then find the polynomial whose zeroes are 𝛼² and 𝛽².
Solution:
Given polynomial: 3x^2-8x+2
\rightarrow a=3, b=-8 \ and \ c=2
\alpha+\beta=\dfrac{-b}{a} =\dfrac{8}{3}
\alpha\beta=\dfrac{c}{a}=\dfrac{2}{3}
The required polynomial has zeroes {\alpha}^2 \ and \ {\beta}^2
\alpha^2+\beta^2 =(\alpha+\beta)^2-2\alpha\beta
\alpha^2+\beta^2 =\dfrac{64}{9}-\dfrac{4}{3}
\alpha^2+\beta^2 =\dfrac{52}{9}
\alpha^2\beta^2=(\alpha\beta)^2
\alpha^2\beta^2=\dfrac{4}{9}
Required polynomial:
p(x) = x^2-(\alpha^2+\beta^2)x+\alpha^2\beta^2
p(x) =x^2-\dfrac{52}{9}x+\dfrac{4}{9}
Clear fractions:
p(x) = 9x^2-52x+4
Final Answer: \boxed{ \text{required polynomial is }9x^2-52x+4}
Q27. (A): In an acute angled triangle ABC, if sin A + B − C = 1/2 and cos B + C − A = 1/2, find ∠A, ∠B and ∠C.
Solution:
We know, A + B + C=180^\circ \quad ... (1) (angle sum prop of a triangle)
Given: \sin(A+B-C)= \dfrac{1}{2}
\sin(A+B-C)= \sin 30^\circ
\implies A+B-C = 30^\circ ... (2)
Given: \cos(B+C-A)= \dfrac{1}{2}
\cos(B+C-A)= \cos 60^\circ
\implies B+C-A = 60^\circ ... (3)
Subtracting (2) from (1)
(A+B+C) - (A+B-C) = 180^\circ - 30^\circ
2C = 150^\circ
C = 75^\circ
Subtracting (3) from (1)
(A+B+C) - (B+C-A) = 180^\circ - 60^\circ
2A = 120^\circ
A = 60^\circ
Substituting A and B in (1)
A+B+C = 180^\circ
60^\circ + B + 75^\circ = 180^\circ
B + 135^\circ = 180^\circ
B = 45^\circ
Final Answer: \boxed{A=60^\circ,\ B=45^\circ,\ C=75^\circ}
Q27 (B). Prove that \dfrac{\sin\theta}{(\sec\theta+\tan\theta-1)}+\dfrac{\cos\theta}{(\csc\theta+\cot\theta-1)}=1
Solution:
LHS = \dfrac{\sin\theta}{(\sec\theta+\tan\theta-1)}+\dfrac{\cos\theta}{(\csc\theta+\cot\theta-1)}
LHS = \dfrac{\sin\theta}{(\frac{1}{\cos\theta}+ \frac{\sin \theta}{\cos\theta}-1)}+\dfrac{\cos\theta}{(\frac{1}{\sin\theta}+ \frac{\cos \theta}{\sin\theta}-1)}
LHS = \dfrac{\sin\theta \cdot \cos\theta}{({1}+ {\sin \theta}-{\cos\theta})}+\dfrac{\cos\theta \cdot \sin \theta}{({1}+ {\cos \theta}-{\sin\theta})}
LHS = \sin\theta \cdot \cos\theta \left[ \dfrac{1}{1+ (\sin \theta-\cos\theta)} + \dfrac{1}{1 - (\sin \theta - \cos\theta)} \right]
LHS = \sin\theta \cdot \cos\theta \left[ \dfrac{(1 - (\sin \theta - \cos\theta) + 1+ (\sin \theta-\cos\theta))}{1- (\sin \theta-\cos\theta)^2} \right]
LHS = \sin\theta \cdot \cos\theta \left[ \dfrac{2}{1- (\sin^{2} \theta + \cos^{2}\theta - 2 \sin \theta \cos \theta)} \right]
LHS = \sin\theta \cdot \cos\theta \left[ \dfrac{2}{1- 1 + 2 \sin \theta \cos \theta} \right]
LHS = \sin\theta \cdot \cos\theta \left[ \dfrac{2}{2 \sin \theta \cos \theta} \right]
LHS = \dfrac{2 \sin\theta \cos\theta} {2 \sin\theta \cos\theta}
LHS = 2
LHS = RHS, Hence Proved
Q28. The product of two numbers is 2028 and their H.C.F. is 13. Find all possible pairs of such numbers.
Solution:
Since the HCF of both numbers is 13.
Let the number be 13x and 13y
Given:
Product = 2028
13x \cdot 13y = 2028
169 xy = 2028
xy = 12
All positive values of x and y which give Product 12
(x,y) = (1,12) \ or \ (2, 6) \ or \ (3, 4)
Of the above pairs choosing only the co-prime numbers (Choosing non-co-prime numbers would change the HCF)
\therefore (x, y) = (1,12) and (3,4)
Numbers for (1, 12)
First Number = 13x = 13
Second Number = 13y = 156
Numbers for (1, 12)
First Number = 13x = 13
Second Number = 13y = 156
Numbers for (3, 4)
First Number = 3x = 39
Second Number = 4y = 52
Final Answer: \boxed{\text{All Possible pair of such numbers are (13, 156) and (39, 52).}}
Q29(A). Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the center.
Solution:
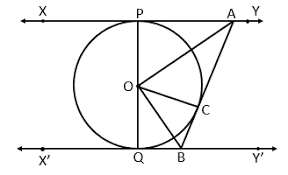
Given: XY \parallel Y'X'
To Prove: \angle AOB = 90^{\circ}
Construction: Join AO and BO
Proof:
In \triangle AOP \ and \ \triangle AOC
\angle APO = \angle ACO = 90^\circ \quad ... (Radius meets the tangent at 90o)
AO = AO \quad ... (Common)
OP = OC \quad ... (Radii)
\therefore \triangle AOP \cong \triangle AOC \quad , Using RHS criteria.
\angle PAO = \angle CAO \quad ... (C.P.C.T.)
Similarly in \triangle OCB \ and \ \triangle OBQ, \angle OBC = \angle OBQ
In Quadrilateral PABQ
\angle P + \angle A + \angle B + \angle Q = 360^\circ
90^\circ + \angle A + \angle B + 90^\circ = 360^\circ
90^\circ + \angle A + \angle B + 90^\circ = 360^\circ
\angle A + \angle B = 180^\circ
\frac{1}{2} \angle A + \frac{1}{2} \angle B = \frac{1}{2} \cdot 180^\circ
\angle OAC + \angle OBC = 90^\circ
\angle OAB + \angle OBA = 90^\circ ... (1)
In \triangle OAB
\angle OAB + \angle OBA + \angle AOB = 180^\circ \quad ... (Angle Sum prop of a triangle)
Using (1)
90^\circ + \angle AOB = 180^\circ
\angle AOB = 90^\circ . Hence Proved
Q29(B). Prove that the length of tangents drawn from an external point to a circle are equal.
Solution:
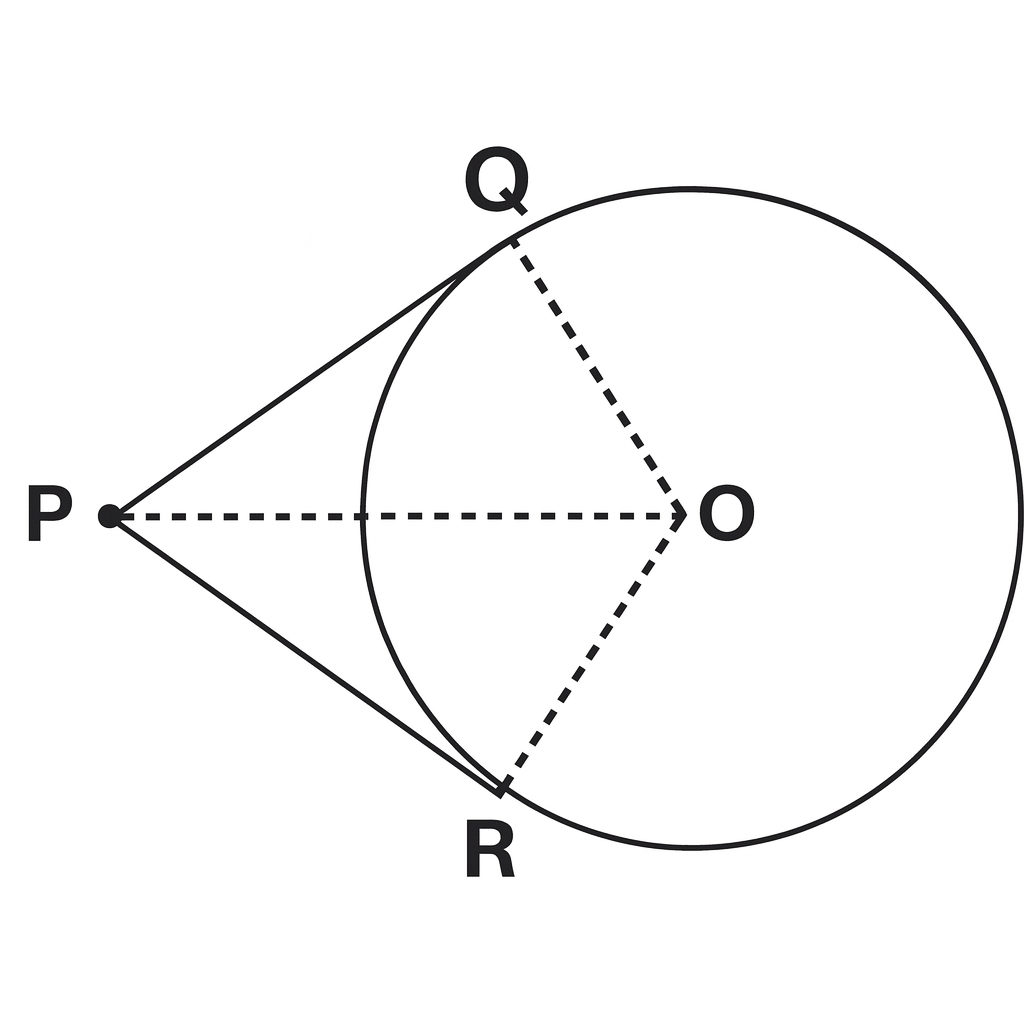
Given: PQ and PR are tangents
To Prove: PQ = PR
Construction: Join OP, OQ and OR
Proof:
In \triangle POQ \ and \ \triangle POR
\angle PQO = \angle PRO = 90^\circ \quad ... (Radius meets the tangent at 90o)
PO = PO \quad ... (common)
QO = RO \quad ... (radii)
\therefore \triangle POQ \cong \triangle POR \quad , Using RHS criteria.
PQ = PR \quad ... (C.P.C.T.)
Therefore PQ = PR. Hence Proved
Q30. Two coins are tossed simultaneously. What is the probability of getting
(i) At least one head?
(ii) At most one tail?
(iii) A head and a tail?
Solution:
Sample space when two coins tosses simultaneously: {HH,HT,TH,TT}
Total number of possible outcomes = 4
(i) At least one head:
Total favourable outcomes = 3, (HH, HT, TH)
Probability of at least one head P(\text {atleast one head }) = \dfrac{3}{4}
(ii) At most one tail:
Total favourable outcomes = 3, (HH, HT, TH)
Probability of atmost one head P(\text {atmost one head} ) = \dfrac{3}{4}
(iii) A head and a tail:
Total favourable outcomes = 2, (HT, TH)
Probability of one head and a tail P(\text {one head and a tail}) = \dfrac{2}{4}=\dfrac{1}{2}
Final Answer: \boxed{\text{(i) } \frac{3}{4},\ \text{(ii) } \frac{3}{4} \ \text{(iii) } \frac{1}{2}}
Q31(A). A train covered a certain distance at a uniform speed. If the train would have been 6 km/h faster, it would have taken 4 hours less than the scheduled time. And, if the train were slower by 6 km/hr; it would have taken 6 hours more than the scheduled time. Find the length of the journey.
Solution:
Let, distance =D,
Case I
Let, speed =v, time t_1=\dfrac{D}{v}.
Case II
Let, speed =v+6, time t_2 = \dfrac{D}{v+6}.
Given: t_1 - t_2 = 4
\dfrac{D}{v} - \dfrac{D}{v+6} = 4
D \left(\dfrac{1}{v} - \dfrac{1}{v+6} \right) = 4
D \left(\dfrac{1}{v} - \dfrac{1}{v+6} \right) = 4
D \dfrac{v+6-v}{v(v+6)} = 4
D \dfrac{6}{v(v+6)} = 4
D = \dfrac{2v(v+6)}{3} ... (1)
Case III
Let, speed =v-6, time t_3 = \dfrac{D}{v-6}.
Given: t_2 - t_1 = 6
\dfrac{D}{v-6} - \frac{D}{v} = 6
D \left( \dfrac{1}{v-6} - \frac{1}{v} \right) = 6
D \left( \dfrac{v-(v-6)}{v(v-6)} \right) = 6
D \left( \dfrac{v-(v-6)}{v(v-6)} \right) = 6
D \left( \dfrac{6}{v(v-6)} \right) = 6
D = 6 \dfrac{v(v-6)}{6}
D = v(v-6) ... (2)
Equating D from (1) and (2)
\dfrac{2v(v+6)}{3} = v(v-6)
2v(v+6) = 3v(v-6)
2v^2 + 12v = 3v^2 - 18v
0 = v^2 - 30v
v^2 - 30v = 0
v(v - 30) = 0
\Rightarrow v =0 \ \text{and } \ v =30 \text {km/hr}
Substituting v in (2)
D = 30(30-6)
D = 30(24)
D = 720 \ \text{km}
Final Answer: \boxed{ \text{the length of the journey is }720\ \text{km}}
Q31(B). Anuj had some chocolates, and he divided them into two lots A and B. He sold the first lot at the rate of ₹2 for 3 chocolates and the second lot at the rate of ₹1 per chocolate, and got a total of ₹400. If he had sold the first lot at the rate of ₹1 per chocolate, and the second lot at the rate of ₹4 for 5 chocolates, his total collection would have been ₹460. Find the total number of chocolates he had.
Solution:
Let, chocolates in Lot A =a, in Lot B =b.
Case I
Revenue from A at ₹2 for 3 chocolates: \dfrac{2}{3}a
Revenue from B at ₹1 per chocolate: b
Given: \dfrac{2}{3}a+b=400
Multiplying equation by 3
2a+3b=1200\quad ... (1)
Case II
Revenue from A at ₹1 per chocolate: a
Revenue from B at ₹4 for 5 chocolates: \dfrac{4}{5}b
Given: a+\dfrac{4}{5}b=460
Multiplying equation by 5
5a+4b=2300\quad ... (2)
Using Elimination
4\times eq. (1):\ 8a+12b=4800 ... (3)
3\times eq. (2):\ 15a+12b=6900 ... (4)
Subtracting (3) from (4)
(15a+12b) - (8a+12b) = 6900 - 4800
7a=2100
a=300
Substituting a in (1)
2(300)+3b=1200\quad
600+3b=1200\quad
3b=600\quad
b=200\quad
Total chocolates: a+b=300+200=500
Final Answer: \boxed{ \text{total number of chocolates is } 500}
Section D — 5 marks Questions
Q32 (A). 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:
| Number of letter | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| Number of Surnames | 6 | 30 | 40 | 16 | 4 | 4 |
Determine the median number of letters in the surname. Find the mean number of letters in the surnames? Also, find the modal size of the surnames.
Solution:
| Class Interval | f_i | \text{c.f.}_i | x_i | d_1 = x_i - A | f_i \cdot d_i |
| 1-4 | 6 | 6 | 2.5 | -6 | -36 |
| 4-7 | 30 | 36 | 5.5 | -3 | -90 |
| 7-10 | 40 | 76 | 8.5 | 0 | 0 |
| 10-13 | 16 | 92 | 11.5 | 3 | 48 |
| 13-16 | 4 | 96 | 14.5 | 6 | 24 |
| 16-19 | 4 | 100 | 17.5 | 9 | 36 |
| Sum | 100 | -18 |
(i) Finding median
Sum of frequencies n = 100
We find cumulative frequencies, calculated in column \text{c.f.}_i
\frac{n}{2} = 50
\therefore \text{median class} = 7-10
We will use the formula: \text{median} = l + \left[ \dfrac{\frac{n}{2} - cf}{f} \right] \times h
Here l = \text{lower limit of median class} = 7
n = \text{total number of observations} = 100
cf = \text{cumulative frequency of class preceding the median class} = 36
f = \text{frequency of median class} = 40
h = \text{class size} = 3
Substituting values
\text{median} = 7 + \left[ \dfrac{50 - 36}{40} \right] \times 3
\text{median} = 7 + \left[ \dfrac{14}{40} \right] \times 3
\text{median} = 7 + 1.05
\text{median} = 8.05
(ii) Finding Mean
Let Assumed mean, A = 8.5
We will use the formula: \text{mean} = A + \dfrac{\sum f_i \cdot d_i}{ \sum f_i }
\text{mean} = 8.5 + \dfrac{-18}{100}
\text{mean} = 8.5 - 0.18
\text{mean} = 8.32
(iii) Finding Mode
\text{modal class is } 7-10
We use the formula: \text{mode } = l + \left( \dfrac{f_1 - f_0}{2f_1 - f_0 - f_2} \right) \times h
Here Here l = \text{lower limit of modal class} = 7
f_0 = \text{frequency of class preceding the median class} = 30
f_1 = \text{frequency of median class} = 40
f_2 = \text{frequency of class succeeding the median class} = 16
h = \text{class size} = 3
Substituting values:
\text{mode } = 7 + \left( \dfrac{40 - 30}{80 - 30 - 16} \right) \times 3
\text{mode } = 7 + \left( \dfrac{10}{34} \right) \times 3
\text{mode } = 7 + 0.88
\text{mode } = 7 + 0.88
\text{mode } = 7.88
Final Answer: \boxed{ \text{median} = 8.05, \quad \text{mean} = 8.32 , \quad \text{mode} = 7.88 }
Q32(B). The median of the distribution given below is 14.4. Find the values of x and y, if the sum of frequency is 20. Also find the mean.
| Class Interval | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
| Frequency | 4 | x | 5 | y | 1 |
Solution:
Given: Median = 14.4
| Class interval | f_i | cf |
| 0-6 | 4 | 4 |
| 6-12 | x | 4+x |
| 12-18 | 5 | 9+x |
| 18-24 | y | 9+x+y |
| 24-30 | 1 | 10+x+y |
| Sum | 10+x+y |
Given Median = 14.4, \ \implies \ \text{class interval } = 12 - 18
Sum of frequency 'n' = 20
We will use the formula: \text{median} = l + \left[ \dfrac{\frac{n}{2} - cf}{f} \right] \times h
Here l = \text{lower limit of median class} = 12
n = \text{total number of observations} = 10+x+y
cf = \text{cumulative frequency of class preceding the median class} = 4+x
f = \text{frequency of median class} = 5
h = \text{class size} = 6
Substituting the values
14.4 = 12 + \left[ \dfrac{\frac{20}{2} - (4+x)}{5} \right] \times 6
14.4 = 12 + \left[ \dfrac{10 - (4+x)}{5} \right] \times 6
14.4 = 12 + \left[ \dfrac{10 - (4+x)}{5} \right] \times 6
14.4 - 12 = \left[ \dfrac{10 - (4+x)}{5} \right] \times 6
2.4 = \left[ \dfrac{10 - (4+x)}{5} \right] \times 6
\dfrac{2.4 \times 5}{6} = \left[10 - (4+x) \right]
\dfrac{2.4 \times 5}{6} = 6-x
2 = 6-x
x = 4
Sum = 20
10+x+y = 20
10+4+y = 20
y = 6
Final Answer: \boxed{x = 4, \ y = 6}
Finding Mean
| Class interval | f_i | x_i | d_i = x_i - A | u_i = \frac{d_i}{h} | f_i \cdot u_i |
| 0-6 | 4 | 3 | -12 | -2 | -8 |
| 6-12 | 4 | 9 | -6 | -1 | -4 |
| 12-18 | 5 | 15 | 0 | 0 | 0 |
| 18-24 | 6 | 21 | 6 | 1 | 6 |
| 24-30 | 1 | 27 | 12 | 2 | 2 |
| Sum | 20 | -4 |
Let Assumed Mean, A = 15
Class Interval, h = 6
We will use the formula: \text{mean} = A + \dfrac{\sum f_i \cdot u_i}{ \sum f_i } \times h
\text{mean} = 15 + \dfrac{-4}{20} \times 6
\text{mean} = 15 - 1.2
\text{mean} = 13.8
Final Answer: \boxed{ Mean = 13.8 }
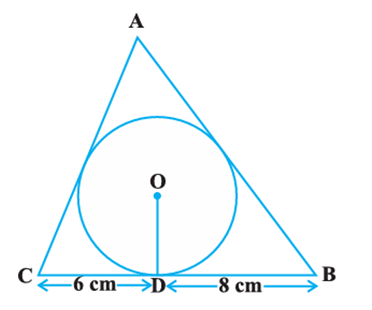
Q33. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig.). Find the sides AB and AC.
Solution:
Given: CD = 6cm, \quad BD = 8cm
Radius OD = 4cm
To Find: AB and AC
Construction: Join O to the point of contact E of circle with tangent AB.
Then Join O to the point of contact (F) of the circle with tangent AC
Join OA, OB and OC
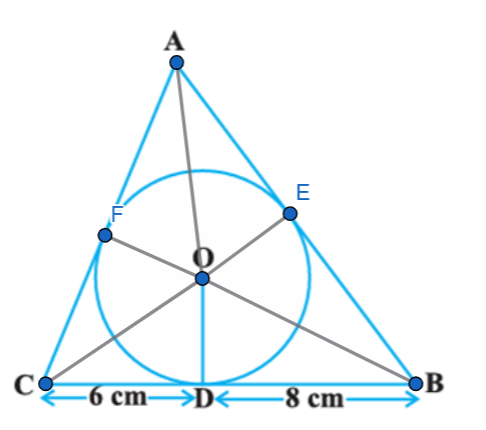
Solution:
Let AE = x
\therefore AF = x \quad ... (Tangents from an external Point area Equal)
Similarly
BD = BE = 8cm \quad ... (Tangents from an external Point area Equal)
CD = CF = 6cm \quad ... (Tangents from an external Point area Equal)
Finding area of triangle using Heron's Formula
Length of sides
a = BC = 14
b = AC = 6+x
c = AB = 8+x
Semi-perimeter s = \frac{a+b+c}{2}
Semi-perimeter s = \frac{14 + 6 + x + 8+ x }{2}
Semi-perimeter s = \frac{28 + 2x}{2}
Semi-perimeter s = 14 + x
Area of \triangle ABC = \sqrt{s(s-a)(s-b)(s-c)}
Area of \triangle ABC = \sqrt{(14+x)(x)(8)(6)} \quad
Area of \triangle ABC = 4\sqrt{(14+x)(x)(3)} \quad ... (1)
In \triangle OCD and \triangle OCF
\angle ODC = \angle OFC = 90^\circ \quad ... (Radius meets the tangent at 90o)
OC = OC \quad ... (Common)
OD = OF \quad ... (radii)
\therefore \triangle OCD \cong \triangle OCF . \quad Using RHS Criteria
\implies \text{Area of } \triangle OCD = \text{Area of } \triangle OCF
Similarly
\implies \text{Area of } \triangle OAF = \text{Area of } \triangle OAE
\implies \text{Area of } \triangle OBD = \text{Area of } \triangle OBE
Finding Area of Triangle
\text{Area of } \triangle ABC = \text{Area of } \triangle OCD \ + \ \text{Area of } \triangle OCF \ + \ \text{Area of } \triangle OAF \ + \ \text{Area of } \triangle OAE \ + \ \text{Area of } \triangle OBD \ + \ \text{Area of } \triangle OBE
\text{Area of } \triangle ABC = 2\text{Area of } \triangle OCD \ + \ 2 \text{Area of } \triangle OAE \ + \ 2\text{Area of } \triangle OBD \
\text{Area of } \triangle ABC = 2 ( \frac{1}{2} \times CD \times OD \ ) + \ 2 ( \frac{1}{2} \times AE \times OE ) \ + \ 2 ( BD \times OD )\
\text{Area of } \triangle ABC = 2 ( \frac{1}{2} \times CD \times OD \ ) + \ 2 ( \frac{1}{2} \times AE \times OE ) \ + \ 2 ( \frac{1}{2} \times BD \times OD ) \
\text{Area of } \triangle ABC = 2 ( \frac{1}{2} \times 6 \times 4 ) \ + \ 2 ( \frac{1}{2} \times x \times 4 ) / + \ 2 (\frac{1}{2}\times 8 \times 4 ) \
\text{Area of } \triangle ABC = 24 + 4x + 32
\text{Area of } \triangle ABC = 56 + 4x ... (2)
Equating Area of Triangle usin (1) and (2)
56 + 4x = 4\sqrt{(14+x)(x)(3)}
14 + x = \sqrt{(14+x)(x)(3)}
Squaring both sides
196 + 28x + x^2 = 3x(14 + x)
196 + 28x + x^2 = 42x + 3x^2
0 = 14x + 2x^2 - 196
x^2 + 7x - 98 = 0
x^2 + 14x -7x - 98 = 0
x(x + 14) -7(x + 14) = 0
(x + 14)(x - 7) = 0
\implies x = -14 and x = 7
Since -ve value is not valid for length, therefore x = 7cm
AB = x+8 = 15cm
AC = x+6 = 13cm
Final Answer: \boxed{ AB = 15cm \ \ and \ \ AC = 13cm }
Q34(A). The entry ticket of an amusement park for adults and children is Rs 480 and Rs 150 respectively. From sale of 450 tickets a total of Rs 1,33,500 was collected.
(i) Find the number of children who attended the park and also the number of adults of adults who attended the park.
(ii) Find the total amount collected if the number of adults and children attending was increased by 50 each.
Solution,
Given:
Adult ticket price is Rs 480,
child ticket price is Rs 150.
(i) Let, the number of adults be x
Let, the number of children be y
Given, total number of tickets sold: 450
x+y = 450 ... (1)
Given, total money collected is Rs 1,34,500
480x+150y = 1,33,500 ... (2)
Multiplying (1) by 150,
150x+150y = 67,500 ... (3)
Subtracting (3) from (2)
(480x+150y) - (150x+150y) = 1,33,500 - 67,500
330x = 66,000
x = 200
Substituting x in (1)
200+y = 450
y = 250
Final Answer:
\boxed{\text{total number of adults is } 200}
\boxed{\text{total number of children is } 250}
(ii)
New Number of adults 200 + 50 = 250
New Number of chidren 250 + 50 = 300
Total Amount collected = 250 \times 480 + 300 \times 150 = 165,000
Final Answer: \boxed{\text{Total amount collected is Rs } 1,65,000 }
Q34(B). Solve the following system of equations graphically for x and y: 3x + 2y = 12; 5x – 2y = 4. Find the co-ordinates of the points where the lines meet the y-axis.
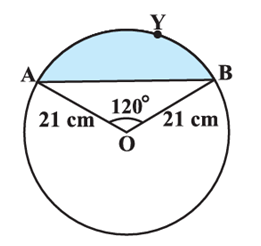
Q35. Find the area of the segment AYB shown in figure, if radius of the circle is 21 cm and \angle AOB=120^\circ. Also find the area of major sector AOB.
Solution:
Given: Radius OB = OA = 21cm
\angle AOB = 120^\circ
To Find: (i) Area of segment AYB
(ii) Area of major sector AOB
Construction: Draw OM \perp AB . \quad As Shown in Fig.
Solution:
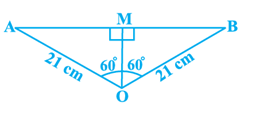
(i). Area of segment AYB = Area of sector OAYB - Area of Triangle OAB ... (1)
In \triangle OAM \ and \ \triangle OBM
\angle OMA = \angle OMB = 90^\circ \quad ... (by construction)
OA = OB \quad ... (radii)
OM = OM \quad ... (common)
\therefore \triangle OAM \cong \triangle OBM \quad ... Using RHS Criteria
\angle AOM = \angle BOM \quad ... (C.P.C.T)
\angle AOM = \angle BOM = 60^\circ
AM = BM \quad ... (C.P.C.T)
In \triangle OMA
\frac{OM}{OA} = \cos 60^\circ
\frac{OM}{21} = \frac{1}{2}
OM = \frac{21}{2} \text{cm}
Also
\frac{AM}{OA} = \sin 60^\circ
\frac{AM}{OA} = \frac{\sqrt{3}}{2}
\frac{AM}{21} = \frac{\sqrt{3}}{2}
AM = \frac{21\sqrt{3}}{2}
AB = 2AM = 21\sqrt{3} cm
So, Area of \triangle OAB = \dfrac{1}{2} AB \times OM
Area of \triangle OAB = \dfrac{1}{2} 21\sqrt{3} \times \frac{21}{2} \text{cm}^2
Area of \triangle OAB = \dfrac{441}{4} \sqrt{3} \text{cm}^2 ... (2)
Area of Sector OAYB = \frac{120}{360} \times \frac{22}{7} \times 21 \times 21
Area of Sector OAYB = 462 \text{ cm}^2 ... (3)
Therefore Using (1), (2) and (3)
Area of segment AYB = \left( 462 - \dfrac{441}{4} \sqrt{3} \right) \text{cm}^2
Area of segment AYB = \dfrac{21}{4}\left( 88 - 21 \sqrt{3} \right) \text{cm}^2
(ii) Area of major sector AOB
Area of major sector AOB = Area of Circle - Area of Minor Sector AOB ... (4)
Area of Circle = \dfrac{22}{7} \times 21 \times 21
Area of Circle = 1386 \text{cm}^2 \quad ... (5)
Using (3), (4) and (5)
Area of major sector AOB = 1386 - 462
Area of major sector AOB = 924 \text {cm}^2
Final Answer: \boxed { \text{Area of segment } AYB = \dfrac{21}{4}\left( 88 - 21 \sqrt{3} \right) \text{cm}^2 }
\boxed{ \text{Area of major sector } AOB = 924 \text {cm}^2 }
Section E — Case Based study Questions 4 marks (1+1+2)
Q36. Answer the following questions based on the information given below. Rohan and Mohini start a passing game with 3 marbles, in the first pass Rohan gives mohini 3 marbles. Then Mohini adds 4 marbles in the second pass and gives 7 marbles to Rohan, he then adds 4 more marbles and gives 11 marbles to Mohini in the third pass, who again adds 4 more marbles and gives 15 marbles to Rohan and this goes on
(i) How many marbles were passed by Rohan to Mohini in 9th pass?
(ii) In which pass were 55 marbles passed?
(iii) (A) If the first person to receive more than 100 marbles wins the game, then who wins the game? Show your work
OR
(iii) (B) Their friend Asna is taking note of the number of marbles passed in each turn and adding all the numbers to reach a sum. Find the sum she reaches after 17 turns.
Solution:
Sequence of marbles passed each turn is arithmetic:
first term a=3, common difference d=4.
General term: a_n=a+(n-1)d=3+4(n-1).
(i) 9th pass (Rohan→Mohini):
a_9=3+4\cdot 8=35
Final Answer: \boxed {\text{Number of marbles passed by Rohan to Mohini is } 35}
(ii) Given a_n=55
3+4(n-1)=55
4(n-1)=52
n -1 =13
n =14
Final Answer: \boxed {\text{55 marbles were passed in turn number } 14}
(iii-A) First term exceeding 100:
a_n > 100
3+4(n-1)>100
4(n-1)>97
n-1> \frac{97}{4}
n > \frac{97}{4} + 1
n > 24.25 + 1
n > 25.25
Integer greater than 25.25 is 26
So 26th pass will have more than 100 marbles
Pass 26 is even, so Mohini gives to Rohan.
Rohan receives T_{26}=3+4\cdot 25=103>100.
Final Answer: \boxed{ \text {Winner: Rohan in the 26th pass} }
(iii-B) Sum of first 17 terms:
S_{17} =\dfrac{17}{2},[2\cdot 3+(17-1)\cdot 4]
S_{17} =\dfrac{17}{2},(6+64)
S_{17} =\dfrac{17}{2}\cdot 70
S_{17} =595
Final Answer: \boxed{\text{Sum after 17 terms is }595}
Q37. Answer the following questions based on the information given below.
In the sport of cricket the Captain sets the field according to a plan. He instructs the players to take a position at a particular place. There are two reasons to set a cricket field—to take wickets and to stop runs being scored. The following graph shows the position of players during a cricket match.
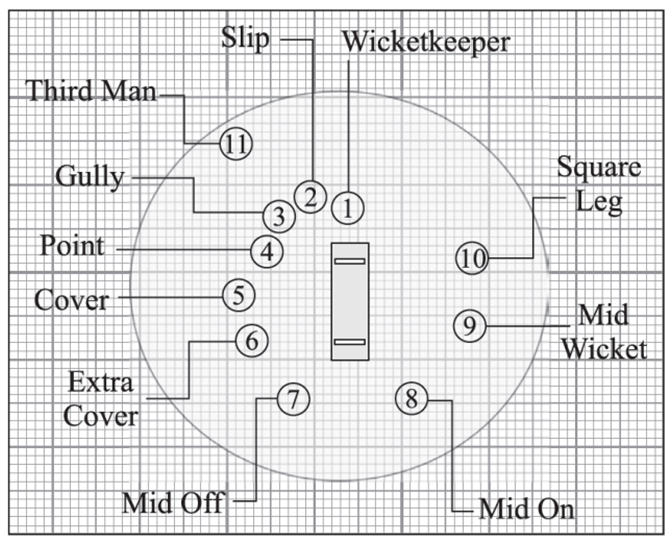
(i). Find the distance between the Wicket keeper W(0,2) and Mid On O(2, -4)
(ii) The Batsman B, is standing at the midpoint of the line joining the Mid-Wicket D(4, -4) of the line joining Third Man T (-4, 4). What are the co-ordinates of the batsman B.
(iii) (A) Find the coordinate of the point on y-axis which is equidistant from the points representing the players at Cover C(–2, 9) and Mid On O(2, -4).
OR
(iii) (B) Find the ratio in which x-axis divides the line segment joining the points Extra Cover E(-3, – 3) and Fine Leg F(2, 7).
Solution:
(i). Distance between the Wicket keeper W(0,2) and Mid On O(2, -4)
D =\sqrt{(2-0)^2+(-4-2)^2}
D =\sqrt{4+36}
D =\sqrt{40}=2\sqrt{10}
Final Answer: \boxed{\text{Distance between the Wicket keeper W(0,2) and Mid On O(2, -4) is } 2\sqrt{10}}
(ii) The Batsman B is standing at the midpoint of the line segment joining Mid-Wicket D(4, -4) and Third Man T(-4, 4).
Finding the coordinates of B.
Using Midpoint formula: x=\dfrac{x_1+x_2}{2}, \ y=\dfrac{y_1+y_2}{2}
B=\left(\dfrac{4+(-4)}{2},\dfrac{-4+4}{2}\right)=(0,0)
Final Answer: \boxed{ \text{Coordinates of batsman are } (0,0)}
(iii) (A) Coordinate of the point on y-axis which is equidistant from the points representing the players at Cover C(–2, 9) and Mid On O(2, -4).
Solution:
Point on y-axis be: P(0, y) .
Equidistant from C(-2,9) and O(2,-4):
i.e. PC = PO
Using distance formula
\sqrt{(0+2)^2+(y-9)^2}=\sqrt{(0-2)^2+(y+4)^2}
Squaring both sides
(2)^2+(y-9)^2=(2)^2+(y+4)^2
(y-9)^2=(y+4)^2
y^2 - 18y + 81 = y^2 + 8y + 16
65 = 26y
y=\dfrac{5}{2}
So point: \left(0,\dfrac{5}{2}\right).
Final Answer: \boxed{ \text{point equidistant from Cover and Mid on is } P\left(0,\frac{5}{2}\right) }
(iii) (A)
Let the ratio in which x-axis divides the line segment joining the points Extra Cover E(-3, –3) and Fine Leg F(2, 7) be k:1
The point of intersection on X axis be Q(x,0)
Using section formula
y=0=\dfrac{k\cdot 7+1\cdot(-3)}{k+1}
0 = 7k-3
k=\frac{3}{7}
\implies k:1= 3:7
Final Answer: \boxed{ \text{X axis divides the lines Joining E and F in the ratio } 3:7 }
Q38. Answer the following questions based on the information given below.
Radio towers are used for transmitting a range of communication services including radio television. The tower will either act as an antenna itself or support one or more antennas on its structure. They are among the tallest human-made structures and are of 2 main types: guyed and self-supporting structures.
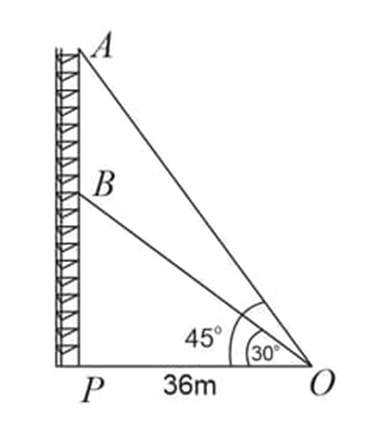
On a similar concept, a radio station was built in two sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 m. From point O, the angle of elevation of the top section B is 30o and the angle of elevation of the top section A is 45o
(i) What is the length of the wire structure from the point O to the top of section B?
(ii) What is the height of the section A from the base of the tower?
(iii) (A) Find the distance AB.
OR
(iii) (B) Find the area of triangle OPB.
Solution:
Given: horizontal distance OP=36\text{ m}.
To top of B: angle 30^\circ. To top of A: angle 45^\circ.
(i) Slant wire OB:
In \triangle OBP
\cos 30^\circ =\dfrac{OP}{OB}
OB =\dfrac{OP}{\cos 30^\circ}
OB =\dfrac{36}{\sqrt{3}/2}
OB =24\sqrt{3}\ \text{m}
Final Answer: \boxed {\text{length of wire is } 24\sqrt{3}\ \text{m}}
(ii) Height of A from base:
In \triangle OAP
\tan 45^\circ = \dfrac{PA}{OP}
PA=OP\tan 45^\circ
PA=36 \cdot 1
=36\ \text{m}
Final Answer: \boxed{ \text{The height of section A is }=36\ \text{m} }
(iii-A) Vertical distance AB
Height of B:
In \triangle OBP
\tan 30^\circ = \dfrac{PB}{OP}
PB=OP\tan 30^\circ
PB = \dfrac{36}{\sqrt{3}}
PB=12\sqrt{3}\ \text{m}
AB=PA-PB=36-12\sqrt{3}\ \text{m}.
AB=12(3-\sqrt{3})\ \text{m}.
Final Answer: \boxed{\text {Distance AB is } 12(3-\sqrt{3})\ \text{m}}
(iii-B) Area of \triangle OPB (right triangle with legs OP and PB):
\text{Area}=\dfrac{1}{2} \times OP \times PB
\text{Area}=\dfrac{1}{2}\cdot 36\cdot 12\sqrt{3}
\text{Area}=216\sqrt{3}\ \text{m}^2
Final Answer: \boxed{ \text{ Area of } \triangle OPB = 216\sqrt{3}\ \text{m}^2}
Class 10 Full Syllabus Practice Question Paper-2 2026 ⇒
Summary
This post provides full Class 10 CBSE Maths Practice Paper-2 2026 Solutions with detailed explanations from Sections A to E. Students can strengthen concepts, revise efficiently, and download the PDF version for offline study before the board exam.
Important Links
Class 12th CBSE Official Sample Papers and Marking Schemes
Class 10th CBSE Official Sample Papers and Marking Schemes
Class 12th ISC Official Specimen Papers and Answer Keys
Class 11th ISC Official Specimen Papers and Answer Keys
Class 10th ICSE Official Specimen Papers and Answer Keys
Class 9th ICSE Official Specimen Papers and Answer Keys