Have you solved Class 12 CBSE Maths Calculus Practice Paper-1 2026 and are looking for a solutions to the questions? Here you’ll find complete, step-by-step NCERT-style solutions for every question. Designed for both students and teachers, these answers make board exam revision easier with clear explanations, formula highlights, and downloadable PDF options.
Class 12 Calculus Practice Question Paper-1 2026 ⇒
Q 1. Evaluate the integral: \int e^{x} \left(\frac{2+ \sin 2x}{1+ \cos 2x} \right) dx
(A) e^x \tan x + C
(B) e^x \cot x + C
(C) e^x (x + \tan x) + C
(D) e^x (x + \cot x) + C
Solution:
I = \int e^{x} \left(\frac{2+ \sin 2x}{1+ \cos 2x} \right) dx
Step 1: Simplify the Trigonometric Expression
Recall the following identities:
\sin 2x = 2 \sin x \cos x
1 + \cos 2x = 2 \cos^2 x
Substitute these values into the numerator and denominator of the integral:
I = \int e^{x} \left(\frac{2+ 2 \sin x \cos x}{2 \cos^2 x} \right) dx
Step 2: Separate the Terms
I = \int e^{x} \left(\frac{2(1+ \sin x \cos x)}{2 \cos^2 x} \right) dx
I = \int e^{x} \left(\frac{1}{\cos^2 x} + \frac{\sin x \cos x)}{ \cos^2 x} \right) dx
Step 3: Convert to Basic Trigonometric Functions
I = \int e^{x} \left(\sec^2 x + \tan x \right) dx
I = \int e^{x} \left(\tan x + \sec^2 x + \right) dx
Step 4: Apply the Special Integral Property
We can now use the standard integration form for exponential functions:
\int e^x [f{x} + f'(x)] dx = e^x f(x) + C
By comparing our current equation to this form, we let:
f(x) = \tan x
Then, f'(x) = \sec^2 x
I = e^x \tan x + C
Correct Option: (A).
Q 2. Find the interval in which f(x)=x^2-4x+5 is increasing
(A) (2, \infty)
(B) (-\infty, 2)
(C) (3, \infty)
(D) (-\infty, \infty)
Solution:
Step 1: Find the Derivative
To find the intervals of increase or decrease, we first find the derivative of the given function f(x) with respect to x.
f(x) = x^2-4x+5
f'(x) = 2x - 4
Step 2: Determine the Condition for Increasing Function
A function is strictly increasing when its derivative is greater than zero:
f'(x) \gt 0
Substitute the value of f'(x):
2x-4 \gt 0
Step 3: Solve for x
2x \gt 4
x \gt 2
This corresponds to the open interval (2, \infty).
Correct Option: (A)
Q 3. If x=a(\cos t+t \sin t) and y=a(\sin t-t \cos t) then find the value of \frac{d^{2}y}{dx^{2}}
(A) \frac{t}{a}\sec^{3}t
(B) at \sec^{3}t
(C) \frac{1}{at}\sec^{3}t
(D) \frac{a}{t}\sec^{3}t
Solution:
Step 1: Differentiate x and y with respect to t.
\frac{dx}{dt} = a(- \sin t + (1 \cdot \sin t + t \cos) )
\frac{dx}{dt} = a(-\sin t + \sin t + t \cos t) = at \cos t
Similarly for y:
\frac{dy}{dt} = a(\cos t -(1 \cdot \cos t + t(-\sin t)))
\frac{dy}{dt} = a(\cos t - \cos t + t \sin t) = at \sin t
Step 2: Find First Derivative dy/dx
\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{at \sin t}{at \cos t} = \tan t
Step 3: Find Second Derivative
Now differentiate \frac{dy}{dx} with respect to x using the chain rule:
\frac{d^2 y}{dx^2} = \frac{d}{dx} (\tan t)
\frac{d^2y}{dx^2} = \sec^2 t \cdot \frac{dt}{dx}
Substitute \frac{dt}{dx} = \frac{1}{\frac{dx}{dt}} = \frac{1}{at \cos t}:
\frac{d^2y}{dx^2} = \sec^2 t \cdot \frac{1}{at \cos t}
\frac{d^2y}{dx^2} = \frac{1}{at} \sec^3 t
Correct Option: (C)
Q 4. What is the position of the particle moving along the parabola y^2=4x at which the rate of increase of the abscissa is twice the rate of increase of the ordinate?
(A) (1, 1)
(B) (2, 2)
(C) (3, 3)
(D) (4, 4)
Solution:
Step 1: Understand the Given Conditions
Equation of the curve: y^2 = 4x
Rate condition: The rate of increase of abscissa (\frac{dx}{dt}) is twice the rate of increase of ordinate (\frac{dy}{dt}).
\frac{dx}{dt} = 2 \frac{dy}{dt}
Step 2: Differentiate the Curve Equation
Differentiate y^2 = 4x with respect to time t:
2y \frac{dy}{dt} = 4 \frac{dx}{dt}
Step 3: Substitute and Solve
Substitute \frac{dx}{dt} = 2 \frac{dy}{dt} into the differentiated equation:
2y \frac{dy}{dt} = 4 \left( 2 \frac{dy}{dt} \right)
2y \frac{dy}{dt} = 8 \frac{dy}{dt}
Assuming the particle is moving (\frac{dy}{dt} \neq 0), we can cancel \frac{dy}{dt}:
2y = 8 \implies y = 4
Step 4: Find x
Put y = 4 back into the curve equation:
(4)^2 = 4x
16 = 4x \implies x = 4
The position is (4, 4).
Correct Option: (D)
Q 5. Find the sum of the order and degree of the differential equation (y''')^{2}+7y^{\prime}-(\cos x)^{2}=0
(A) 5
(B) 2
(C) 3
(D) Not Defined
Solution:
Step 1: Identify Order
The order of a differential equation is the order of the highest derivative present.
Here, the highest derivative is y''' (3rd derivative). Order = 3
Step 2: Identify Degree
The degree is the power of the highest derivative when the equation is a polynomial in derivatives.
The highest derivative y''' has a power of 2. Degree = 2
Step 3: Calculate Sum
\text{Sum} = \text{Order} + \text{Degree} = 3+2 =5
Correct Option: (A)
Q 6. Integrating factor of the differential equation (1-x^2)\frac{dy}{dx}-xy=1 is..
(A) -x
(B) \frac{x}{1+x^2}
(C) \sqrt{1-x^2}
(D) \frac{1}{2}\log(1-x^2)
Solution:
Step 1: Convert to Standard Linear Form
The standard linear differential equation form is \frac{dy}{dx} + Py = Q.
Divide the given equation by 1 - x^2 :
\frac{dy}{dx} - \frac{xy}{1 - x^2}= \frac{1}{1 - x^2}
Here, P = -\frac{x}{1 - x^2}.
Step 2: Calculate Integrating Factor (IF)
The formula for IF is e^{\int P dx}.
\text{I.F.} = e^{\int \frac{-x}{1 - x^2} dx}
Let =1-x^2 = t, then -2x dx = dt \implies -x dx = \frac{dt}{2}.
\int \frac{-x}{1 - x^2} dx = \int \frac{dt}{2t} =\frac{1}{2} \log |t| = \log{ \sqrt{1-x^2}}
Step 3: Simplify
\text{I.F.} = e^{\log \sqrt{1-x^2}}
Using the property e^{\log A} = A:
\text{I.F.} = \sqrt{1-x^2}
Correct Option: (C)
Q 7. The rate of change of the volume of a sphere with respect to its surface area, when its radius is 2 units
(A) 1 unit
(B) 2 units
(C) 3 units
(D) None of these
Solution:
Step 1: State Formulas
Volume of sphere (V) = \frac{4}{3}\pi r^3
Surface Area of sphere (S) = 4\pi r^2
Step 2: Differentiate with respect to radius r
\frac{dV}{dr} = \frac{4}{3} \pi (3r^2) = 4\pi r^2
\frac{dS}{dr} = 4\pi (2r) = 8\pi r
Step 3: Find Rate of Change of V with respect to S
We need to find \frac{dV}{dS}.
\frac{dV}{dS} = \frac{\frac{dV}{dr}}{\frac{ds}{dr}}
\frac{dV}{dS} = \frac{4\pi r^2}{8\pi r} = \frac{r}{2}
Step 4: Evaluate at r = 2
\left. \frac{dV}{dS} \right|_{r=2} = \frac{2}{2} = 1
Correct Option: (A)
Section B (2 Marks Each)
Q 8. Determine the value of k for which the following function is continuous at x=3
f(x)=\begin{cases}\frac{(x+3)^{2}-36}{x-3}, &x\ne3 \\ k, &x=3 \end{cases}
Solution:
Step 1: Condition for Continuity
For the function to be continuous at x=3, the limit of the function as x \to 3 must equal the value of the function at x=3.
\lim_{x \to 3} f(x) = f(3) = k
Step 2: Evaluate the Limit Substitute the function expression:
\lim_{x \to 3} \frac{(x+3)^2 - 36}{x-3}
This is a \frac{0}{0} form.
We can simplify using the difference of squares formula a^2 - b^2 = (a-b)(a+b):
\lim_{x \to 3} \frac{((x+3) - 6)((x+3) + 6)}{x-3}
\lim_{x \to 3} \frac{(x-3)(x+9)}{x-3}
\lim_{x \to 3} (x+9) = 3+9 = 12
Step 3: Equate to k
Since the limit is 12, for continuity, k must be 12.
Final Answer: \boxed{ k = 12 }
9. Differentiate \tan^{-1}\left(\frac{1+\cos x}{\sin x}\right) with respect to x
Solution:
Step 1: Simplify the Argument using Half-Angle Formulas
Let y = \tan^{-1}\left(\frac{1+\cos x}{\sin x}\right).
Recall the identities:
1 + \cos x = 2 \cos^2 \frac{x}{2}
\sin x = 2 \sin \frac{x}{2} \cos \frac{x}{2}
Substitute these into the expression:
y = \tan^{-1}\left(\frac{2 \cos^2 \frac{x}{2}}{2 \sin \frac{x}{2} \cos \frac{x}{2}}\right)
Step 2: Simplify Trigonometric Ratios
y = \tan^{-1}\left(\frac{\cos \frac{x}{2}}{\sin \frac{x}{2}}\right)
y = \tan^{-1}\left(\cot \frac{x}{2} \right)
y = \tan^{-1}\left(\tan (\frac{\pi}{2} - \frac{x}{2}) \right)
Step 3: Differentiate
y = \frac{\pi}{2} - \frac{x}{2}
Differentiating w.r.t x:
\frac{dy}{dx} = 0 - \frac{1}{2}
Final Answer: \boxed { \frac{dy}{dx} = -\frac{1}{2} }
Q 10. Evaluate \int\frac{dx}{\sin^{2}x \cos^{2}x}
Solution:
Step 1: Use Trigonometric Identity in Numerator
We know that 1 = \sin^2 x + \cos^2 x.
Substitute this in the numerator:
I = \int\frac{\sin^2 x + \cos^2 x}{\sin^{2}x \cos^{2}x} dx
Step 2: Split the Integral
I = \int \left( \frac{\sin^2 x}{\sin^{2}x \cos^{2}x} + \frac{\cos^2 x}{\sin^{2}x \cos^{2}x} \right) dx
I = \int \left( \frac{1}{\cos^2 x} + \frac{1}{\sin^2 x} \right) dx
Step 3: Integrate Standard Forms
I = \int (\sec^2 x + \cosec^2 x) dx
I = \tan x - \cot x + C
Final Answer: \boxed{ \int\frac{dx}{\sin^{2}x \cos^{2}x} = \tan x - \cot x + C }
Q 11. Using integration, find the area bounded by the curve x^2=4y, \ x=2 and the X axis in the First Quadrant.
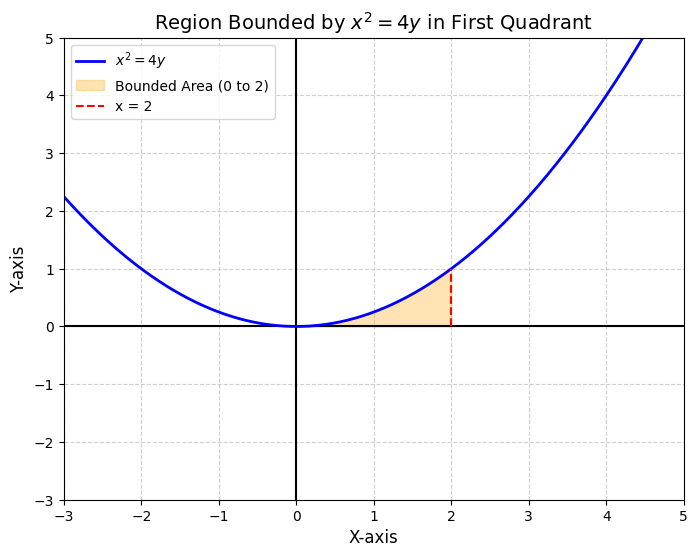
Solution:
Step 1: Set up the Integral
Curve: y = \frac{x^2}{4}.
Limits: x=0 to x=2 (First Quadrant).
A = \int_{0}^{2} y \ dx
A = \int_{0}^{2} \frac{x^2}{4} \ dx
Step 2: Integrate
A = \frac{1}{4} \left[\frac{x^3}{3} \right]_0^2
A = \frac{1}{12} [2^3 - 0^3] = \frac{8}{12}
A = \frac{2}{3} \text{ sq. units}
Final Answer: \boxed{\text{Area: } = \frac{2}{3} \text{ sq. units} }
Q 12. Find the general solution of the differential equation \frac{dy}{dx}=\frac{1+y^{2}}{1+x^{2}}
Solution:
Step 1: Separate Variables
Bring y terms to the LHS and x terms to the RHS:
\frac{dy}{1+y^{2}}=\frac{dx}{1+x^{2}}
Step 2: Integrate Both Sides
\int \frac{dy}{1+y^{2}}= \int \frac{dx}{1+x^{2}}
Using the standard formula \int \frac{dx}{1+x^2} = \tan^{-1}x:
\tan^{-1} y = \tan^{-1}x + C
Final Answer: \boxed{\text{General Solution: } \tan^{-1} y = \tan^{-1}x + C }
Section C (3 Marks Each)
Q 13. If y=(x+\sqrt{1+x^2})^{n}, then show that (1+x^2)\frac{d^{2}y}{dx^{2}}+x\frac{dy}{dx}=n^{2}y
Solution:
Step 1: Finding first Derivative:
\frac{dy}{dx} = n(x+\sqrt{1+x^2})^{n-1} \cdot \left(1+\frac{1}{2\sqrt{1+x^2}} \cdot 2x \right)
\frac{dy}{dx} = n(x+\sqrt{1+x^2})^{n-1} \cdot \left(\frac{\sqrt{1+x^2} + x}{\sqrt{1+x^2}}\right)
\frac{dy}{dx} = \frac{n(x+\sqrt{1+x^2})^{n}}{\sqrt{1+x^2}}
\frac{dy}{dx} = \frac{ny}{\sqrt{1+x^2}}
Step 2: Rearrange and Square
\sqrt{1+x^2} \frac{dy}{dx} = ny
Squaring both sides:
(1+x^2) \left( \frac{dy}{dx} \right)^2 = n^2y^2
Step 3: Differentiate Again Implicitly
Differentiate w.r.t x:
(1+x^2) \cdot 2\frac{dy}{dx} \cdot \frac{d^2y}{dx^2} + \left( \frac{dy}{dx} \right)^2 \cdot 2x = n^2 \cdot 2y \frac{dy}{dx}
Divide the entire equation by 2\frac{dy}{dx}:
(1+x^2) \cdot \frac{d^2y}{dx^2} + x \frac{dy}{dx} = n^2 y
Hence Shown.
Q 14. Show that the function f(x)=|x+1|+|x-1| is not differentiable at x=-1 and x=1
Solution:
Step 1: Define the Function in Intervals
First, we express the modulus function explicitly based on the critical points x = -1 and x = 1.
Case 1 (x < -1): Both terms are negative.
f(x)=-(x+1)-(x-1) = -x-1-x+1 = -2x
Case 2 (-1 \le x < 1): First term is positive, second is negative.
f(x)=(x+1)-(x-1) = x+1-x+1 = 2
Case 3 (x \ge 1): Both terms are positive.
f(x)=(x+1)+(x-1) = x+1+x-1 = 2x
So, the function is defined as:
f(x) = \begin{cases} -2x, \ x\lt -1 \\ 2, \ -1 \le x \lt 1 \\ 2x, \ x \ge 1 \end {cases}
Step 2: Check Differentiability at x = -1
We use the limit formula for derivatives: f'(c) = \lim_{h \to 0} \frac{f(c+h) - f(c)}{h}.
Here, c = -1 and f(-1) = 2.
(i) Left Hand Derivative (LHD) at x = -1
For LHD, h < 0, so x = -1+h lies in the region x < -1.
We use f(x) = -2x.
\text{LHD} = \lim_{h \to 0^-} \frac{f(-1+h) - f(-1)} {h}
\text{LHD} = \lim_{h \to 0^-} \frac{-2(-1+h) - 2}{h}
\text{LHD} = \lim_{h \to 0^-} \frac{2 -2h - 2}{h}
\text{LHD} = \lim_{h \to 0^-} \frac{-2h}{h} = -2
(ii) Right Hand Derivative (RHD) at x = -1
For RHD, h > 0, so x = -1+h lies in the region -1 \le x < 1.
We use f(x) = 2.
\text{RHD} = \lim_{h \to 0^+} \frac{f(-1+h) - f(-1)}{h}
\text{RHD} = \lim_{h \to 0^+} \frac{2 - 2}{h}
\text{RHD} = \lim_{h \to 0^+} \frac{0}{h} = 0
Conclusion for x = -1:
Since \text{LHD} \neq \text{RHD} (-2 \neq 0), the function is not differentiable at x = -1.
Step 3: Check Differentiability at x = 1
Here, c = 1 and f(1) = 2(1) = 2.
(i) Left Hand Derivative (LHD) at x = 1
For LHD, h < 0, so x = 1+h lies in the region -1 \le x < 1.
We use f(x) = 2.
\text{LHD} = \lim_{h \to 0^-} \frac{f(1+h) - f(1)}{h}
\text{LHD} = \lim_{h \to 0^-} \frac{2 - 2}{h} = 0
(ii) Right Hand Derivative (RHD) at x = 1
For RHD, h > 0, so x = 1+h lies in the region x \ge 1.
We use f(x) = 2x.
\text{RHD} = \lim_{h \to 0^+} \frac{f(1+h) - f(1)}{h}
\text{RHD} = \lim_{h \to 0^+} \frac{2(1+h) - 2}{h}
\text{RHD} = \lim_{h \to 0^+} \frac{2 + 2h - 2}{h}
= \lim_{h \to 0^+} \frac{2h}{h} = 2
Conclusion for x = 1:
Since \text{LHD} \neq \text{RHD} (0 \neq 2), the function is not differentiable at x = 1.
Q 15. Using integration, find the area of the region bounded by y=|x+1|+1, x=-3, x=3 and y=0
Solution:
Step 1: Define the Modulus Function
The critical point for |x+1| is x = -1.
Case 1: x \ge -1 implies y = (x+1) + 1 = x+2
Case 2: x < -1 implies y = -(x+1) + 1 = -x
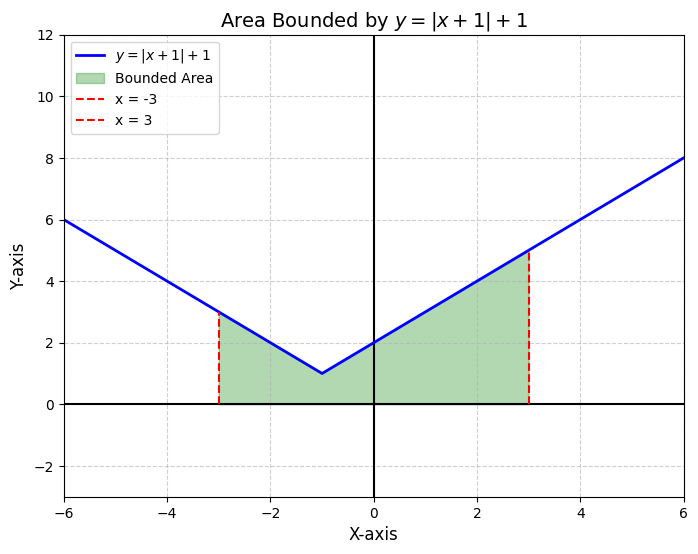
Step 2: Set up the Definite Integral
Split the integral at the critical point x = -1:
A = \int_{-3}^{-1} (-x) dx + \int_{-1}^{3} (x+2) \ dx
Step 3: Integrate and Solve
Part 1: \left[ -\frac{x^2}{2} \right]_{-3}^{-1} = (-\frac{1}{2}) - (-\frac{9}{2}) = 4
Part 2: \left[ \frac{x^2}{2} + 2x \right]_{-1}^{3} = (\frac{9}{2} + 6) - (\frac{1}{2} - 2) = 10.5 - (-1.5) = 12
Total Area = 4 + 12 = 16 sq. units
Final Answer: \boxed{ \text{Total Area } = 16 \text{sq. units. } }
Section D (5 Marks Each)
Q 16. Evaluate \int(x+3)\sqrt{3-4x-x^{2}}dx
Solution:
Step 1: Express Linear Term in terms of Derivative of Quadratic
Let x+3 = A \frac{d}{dx}(3-4x-x^2) + B
x+3 = A (-4-2x) + B
Comparing coefficients:
-2A = 1 \implies A = -1/2
-4A + B = 3 \implies -4(-1/2) + B = 3 \implies 2 + B = 3 \implies B = 1
Rewrite the integral I:
I = -\frac{1}{2} \int (-4-2x) \sqrt{3-4x-x^{2}}dx + \int \sqrt{3-4x-x^2} dx
Step 2: Solve First Integral
I_1 = -\frac{1}{2} \int (-4-2x) \sqrt{3-4x-x^{2}}dx
Let 3-4x-x^2 = t, then (-4-2x)dx = dt.
I_1 = -\frac{1}{2} \int t^{1/2} dt
I_1 = -\frac{1}{2} \cdot \frac{2}{3} t^{3/2}
I_1 = -\frac{1}{3} (3-4x-x^{2})^{3/2}
Step 3: Solve Second Integral
I_2 = \int \sqrt{3-4x-x^2} dx
Complete the square for 3-4x-x^2
3-4x-x^2 = 3 - (x^2 + 4x) = 3 - (x^2 + 4x + 4 - 4) = 7 - (x+ 2)^2
I_2 = \int \sqrt{(\sqrt{7})^2 - (x+2)^2} dx
Using standard formula \int \sqrt{a^2-x^2} dx = \frac{x}{2}\sqrt{a^2-x^2} + \frac{a^2}{2}\sin^{-1}\frac{x}{a}:
I_2 = \frac{x+2}{2} \sqrt{3-4x-x^2} + \frac{7}{2} \sin^{-1} \left(\frac{x+2} {\sqrt {7}} \right)
I = I_1 + I_2
I = -\frac{1}{3} (3-4x-x^{2})^{3/2} + \frac{x+2}{2} \sqrt{3-4x-x^2} + \frac{7}{2} \sin^{-1} \left(\frac{x+2} {\sqrt {7}} \right) + C
Final Answer: \boxed{ \int(x+3)\sqrt{3-4x-x^{2}}dx = -\frac{1}{3} (3-4x-x^{2})^{3/2} + \frac{x+2}{2} \sqrt{3-4x-x^2} + \frac{7}{2} \sin^{-1} \left(\frac{x+2} {\sqrt {7}} \right) + C }
Q 17. Solve the differential equation x dy-y dx=\sqrt{x^{2}+y^{2}} dx given y=0 when x=1
Solution:
Step 1: Simplify to Homogeneous Form
x dy=(y + \sqrt{x^{2}+y^{2}}) dx
\frac{dy}{dx} = \frac{y}{x} + \frac{\sqrt{x^2+y^2}}{x} = \frac{y}{x} + \sqrt{1+\left(\frac{y}{x}\right)^2}
Step 2: Substitution
Let y = vx, so \frac{dy}{dx} = v + x\frac{dv}{dx}.
v + x \frac{dv}{dx} = v + \sqrt{1+v^2}
x\frac{dv}{dx} = \sqrt{1+v^2}
Step 3: Integrate
\int \frac{dv}{\sqrt{1+v^2}} = \int \frac{dx}{x}
\log|v + \sqrt{1+v^2}| = \log|x| + \log C
\log|v + \sqrt{1+v^2}| = \log|Cx|
v + \sqrt{1+v^2} = Cx
Replace v = y/x:
\frac{y}{x} + \sqrt{1+\frac{y^2}{x^2}} = Cx
\frac{y + \sqrt{x^2+y^2}}{x} = Cx
y + \sqrt{x^2+y^2} = Cx^2 … (1)
Step 4: Particular Solution
Given y=0 when x=1:
0 + \sqrt{1+0} = C(1)^2 \implies 1=C
Substituting C in (1)
y + \sqrt{x^2+y^2} = x^2
Final Answer: \boxed{ y + \sqrt{x^2+y^2} = x^2 }
Section E (Case Study)
18. Case Study: Window Design
Dr. Anuradha residing in Chandigarh went to see an apartment of 3 BHK sector 31. The window of the house was in the form of a rectangle surmounted by a semicircular opening having a perimeter of the window 10 m in as shown in the figure below:
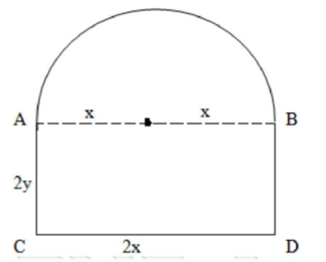
Based on the above information answer the following:
(i) Find the relation between x and y
(ii) Express the area ‘A’ of the window as a function of x
(iii) (A) For what value of x will the window have maximum area?
OR
(iii) (B) For what value of y will the window have maximum area?
Solution:
Dimensions: Rectangle width 2x, Rectangle height 2y (Sides AD and BC are 2y, CD is 2x).
(i) Find the relation between x and y The perimeter consists of the three sides of the rectangle plus the circumference of the semi-circle.
Base = 2x
Two vertical sides = 2y + 2y = 4y
Semi-circle arc length (radius is x) = \pi x
P = 2x + 4y + \pi x = 10
(2+\pi)x + 4y = 10
y = \frac{10 - (2+\pi)x}{4}
\boxed{ y = \frac{10 - (2+\pi)x}{4}}
(ii) Express the area ‘A’ of the window as a function of x
Area = Area of Rectangle + Area of Semi-circle
A =(2x)(2y) + \frac{1}{2} \pi x^2
A = 4xy + \frac{1}{2} \pi x^2
Substitute y from part (i):
A = 4x \left( \frac{10 - (2+\pi)x}{4} \right) + \frac{1}{2} \pi x^2
A(x) = 10x - (2+\pi)x^2 + 0.5\pi x^2
A(x) = 10x - 2x^2 - \pi x^2 + 0.5\pi x^2
A(x) = 10x - 2x^2 - \frac{\pi}{2}x^2
\boxed{A(x) = 10x - 2x^2 - \frac{\pi}{2}x^2}
(iii) A: For what value of x will the window have maximum area?
To maximize area, find A'(x) and set to 0.
A'(x) = 10 - 4x - \pi x
10 - x(4+\pi) = 0
x = \frac{10}{4+\pi}
(Checking second derivative: A''(x) = -4 - \pi < 0, so it is a maximum).
Value of x for maximum Area = \frac{10}{4+\pi} meters.
Final Answer: \boxed{x = \frac{10}{4+\pi}}
(iii) (B) For what value of y will the window have maximum area?
Solution:
Step 1: Identify the Area and Perimeter Equations
From Part (iii) A we have x = \frac{10}{4+\pi}
Step 2: Substitute x in y
From part (i) y = \frac{10 - (2+\pi)x}{4}
Substituting x
y = \frac{10 - (2+\pi)\frac{10}{4+\pi}}{4}
y = \frac{10[4 + \pi - (2 + \pi)]}{4(4+ \pi)}
y = \frac{10 \cdot 2}{4(4+ \pi)}
y = \frac{5}{(4+ \pi)}
Value of y for maximum Area y = \frac{5}{(4+ \pi)}
Final Answer: \boxed{y = \frac{5}{(4+ \pi)}}
